All One Problem (with 1000 binary genes, assuming 1 is good gene while 0 is not.
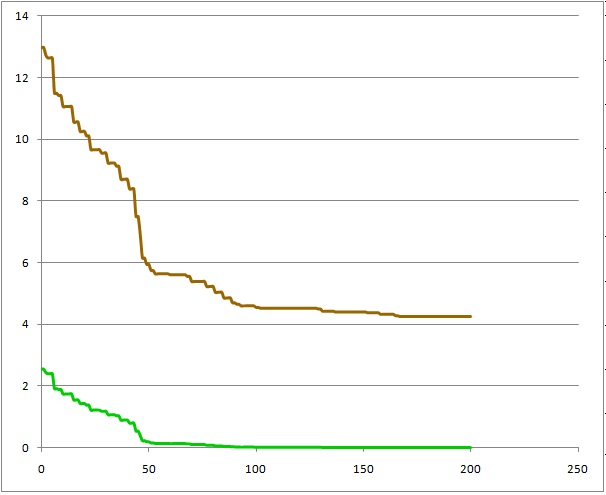
=> We can see the number of good genes '1' increase as evelution goes. But we need to be lucky to obtain all '1' chromosomes when number of population is small, say, 100.
Then what will happen if the number of good gene '1' is extremely few, say, 0.1% instead of 50%? Assuming one chromosome has 1000 genes, average number of good gene '1' at the begining is only 1 while number of gene '0' being 999.
(i) Population number: 100 vs. 7000 ... By Potapchuk Sergey
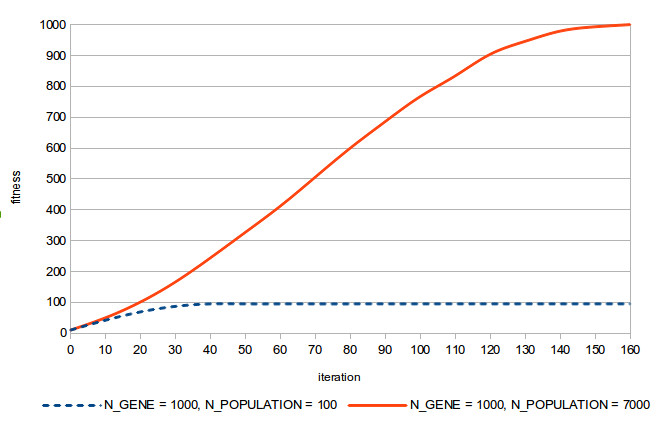
=> Quite amazingly, the number of '1' increases but when the initial population is small such as 100 it saturates immatualy. One way to avoid this immatured saturation (called "Local Optimum"), we might increase the number of population. See, the number of '1' in the best chromosome in each population vs. generation.
(ii) Population number: 100, 1000, 3000, 5000, 6500 and 9000 ... Doronin Nikolai
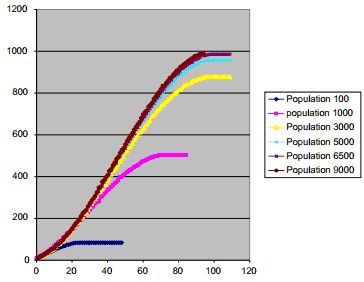
=> We can see that all the genes in the best chromosom are '1' if we start with an enough amount of initial population.
(i) Mutate genes an average of one out of thousand (mutation rate is 0.001) in a similar evolution of 1000 gene chromosomes with '1' and '0' both being 50% ... Meshco Evgenii
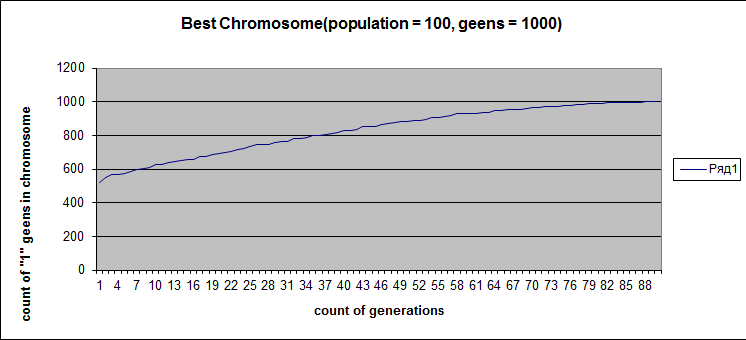
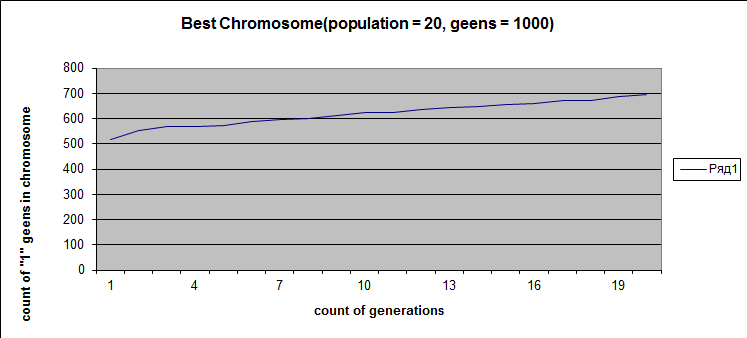
=> When we have mutation we can see that much smaller population is enough to obtain the solution than evolution without mutation. In this example, number of population 100 lead to success while 20 was too small to reach all-one chromosome.
(ii) Or, experiment to know how population size influences the result ... By Bogush Anatoluy
=> When we have mutation we can see that much smaller population is enough to obtain the solution than evolution without mutation. See even 50 chromosomes evolved to all one chromosomes.
Multi-dimensional function minimization
(i) An evolution without mutation of a population of 100 chromosome of 20 real-number genes ... By Vyshinskaya Natalia
=> This task is easy enough and as such mutation is not necessary.
(ii) What if we apply mutation? ... By Yankovich Aleksandr
=> We can see a mutation makes a evolution a little faster, not so dramatically, though.
Many many local minimum (smaller value of y than neibhour points but not minimum) surround the global minimum (real minimum).
(i) Results with number of chromosomos in population 20 (Left), 50 (Center) and 100 (Right) ... By Yarashuk Alex
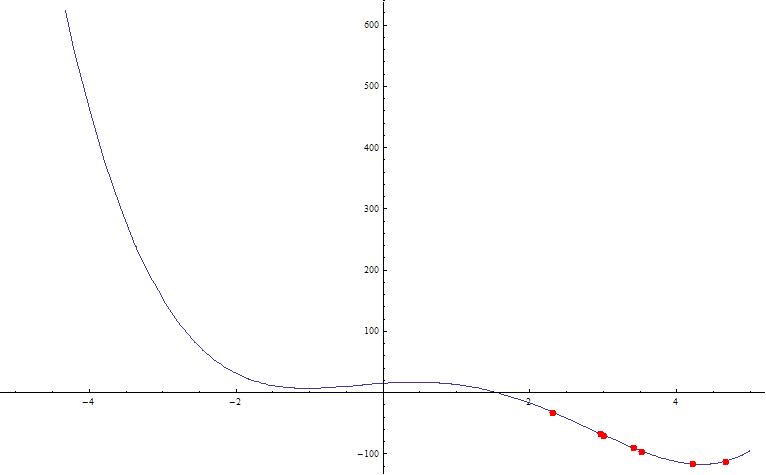
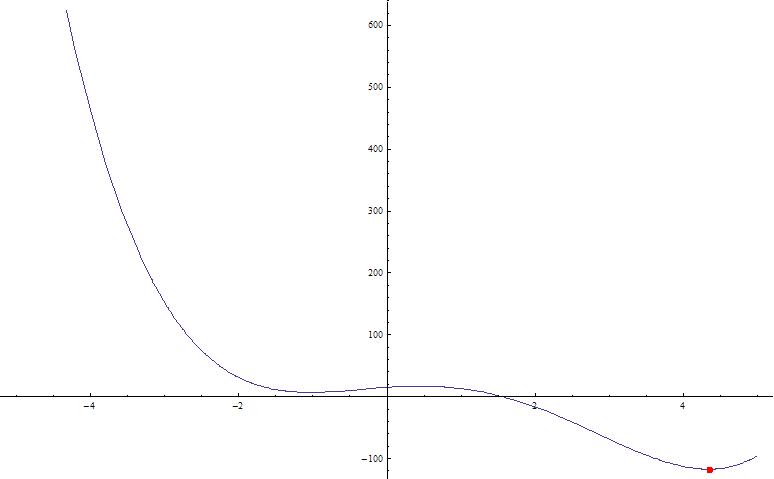
=> When population is small all chromosomes are trapped in a local minimum. It reeaches global minimum with 100 chromosomes.
(ii) Results with mutation ... By Ryshchuk Arcadzi
2-dimensional function minimization
All the binary chromosomes to apply 2-D graph are also shown.
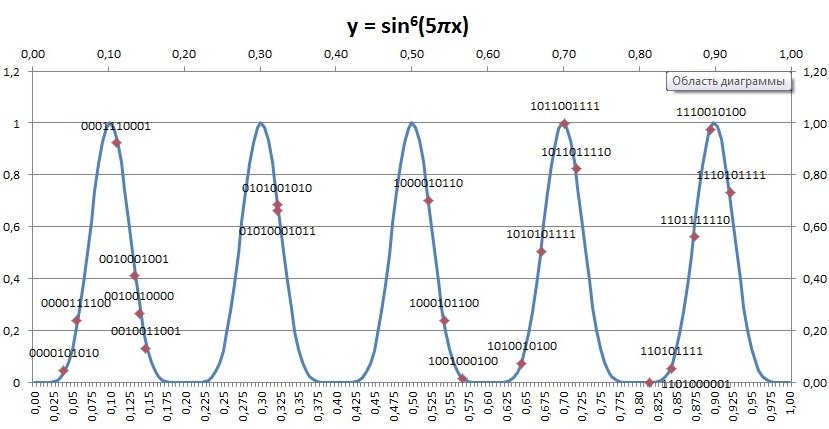
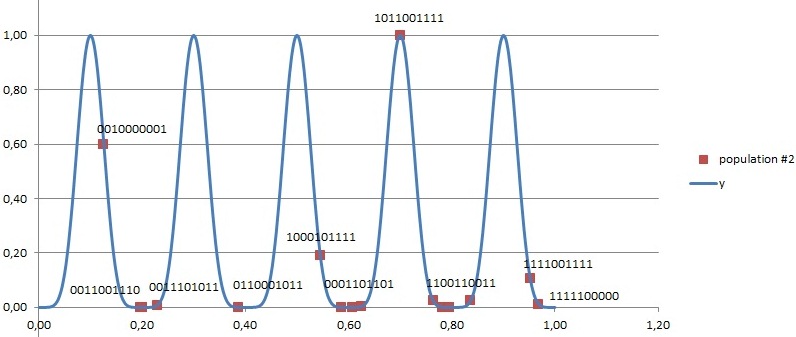
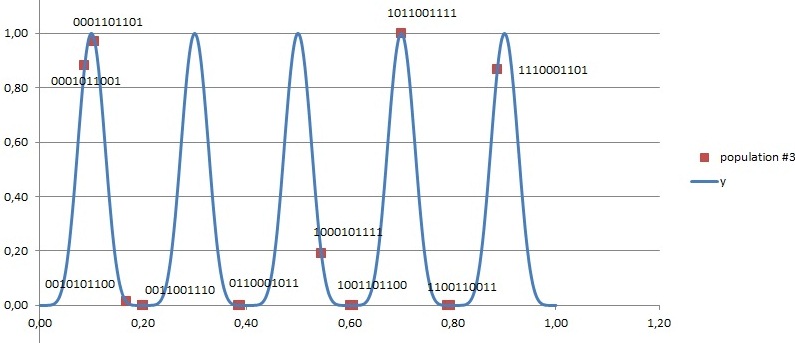
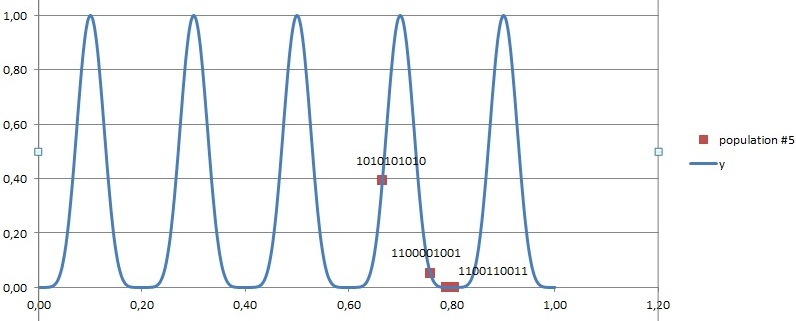
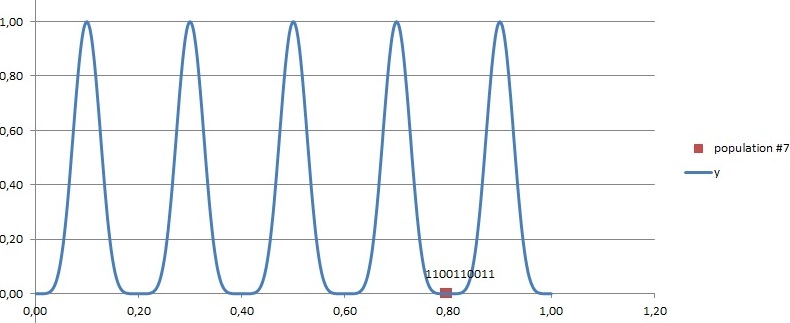
=> All the chromosomes eventually go to one of the six minimum points Like all guys gathered one bottle of vodka (or girl), while there were six bottles (beautiful girls). If we run the algorithm again, those choro mosomes might go the other different minimum (Not shown here though).
Knapsack Problem First, we create N items with price of each of them p_i being at random from 0 to 1 and size w_i being also from 0 to 1 at random, such as:
p_i = 0.32, 0.78, 0.54, ...... & w_i = 0.12, 0.55, 0.38, ......
We pick up items, one item only once, and put them all into one knapsack whose capacity is N/2. Then we want to maximize total price of the items in the knapsack
(i) N=20 ... By Romanyk Oksana
=> Maximum total price seems to be 11.
(ii) N=50 ... By Ryshchuk Arcadzi
=> Maximu total price seems to be 52.
(iii) N=500 ... By Chiruck Dmitrey
=> Maximum total price seems to be 250. To make sure that it's not a local minimum, the program was ran 3 times.
(iv) N=1000 ... By Yarashuk Alex
=> Maximum total price seems to be 500. To make sure that it's not a local minimum, the program was ran 4 times.
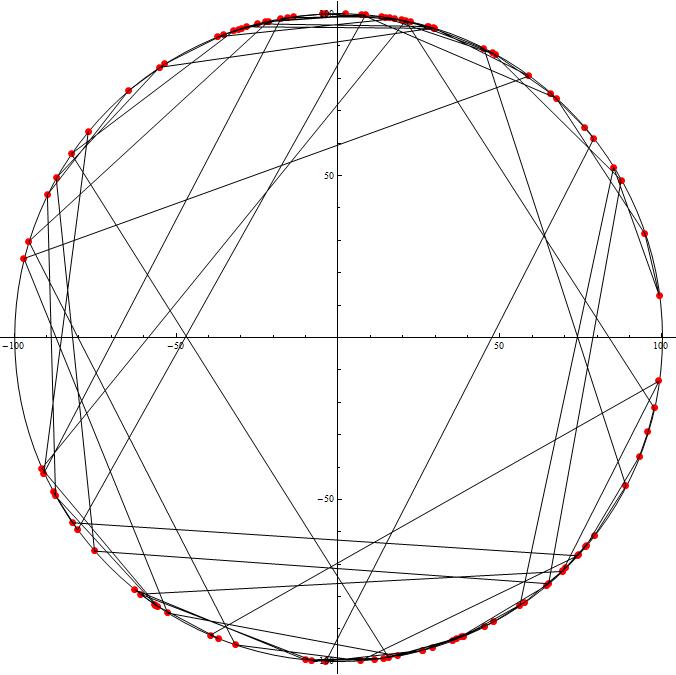
Traveling Selesperson Problem (TSP) => Still under construction (i) A result: Initial random route (Left), Intermediate route (Center) and final shortest route (Right) ... By Kutushina Tatyana
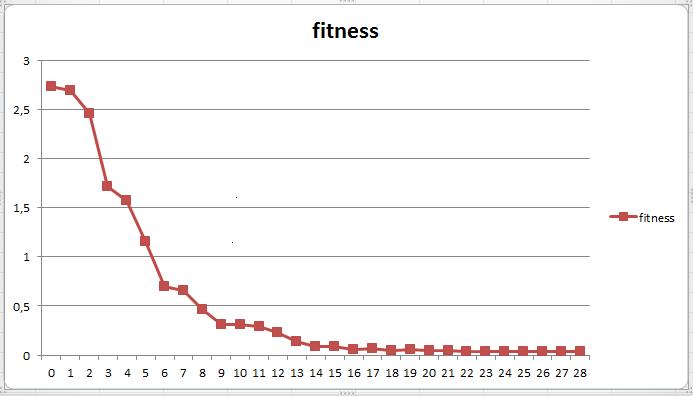
Its fitness vs generation
=> In this case we know the shortest root should always on the circle, and the graph shows a success with quite a shorter generation.
(ii) The other result ... By Baksha Andrey
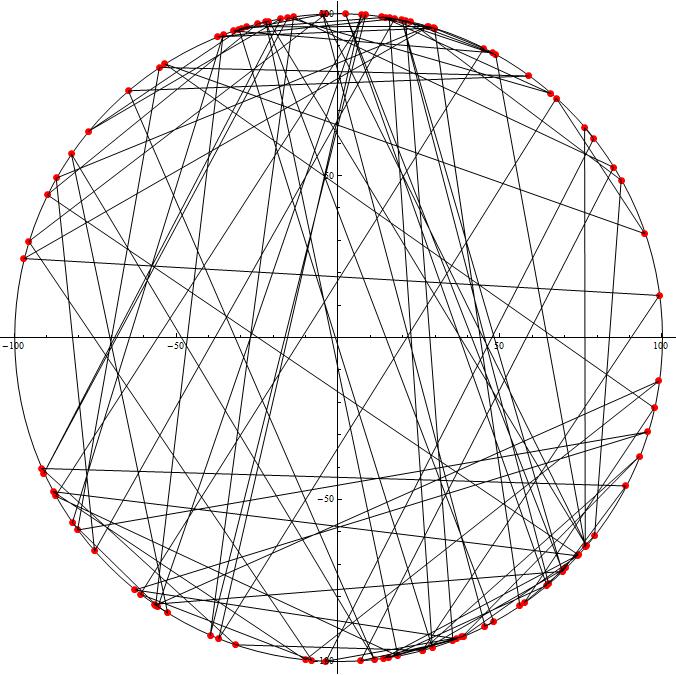
=> It seems to be trapped to a local minimum, but any way the final route is much shorter than the initial random route.
Lucky Dog (i) A result: Initial stupid dogs (Left) and Final lucky dog (Right) ... By Vyshinskaya Natalia
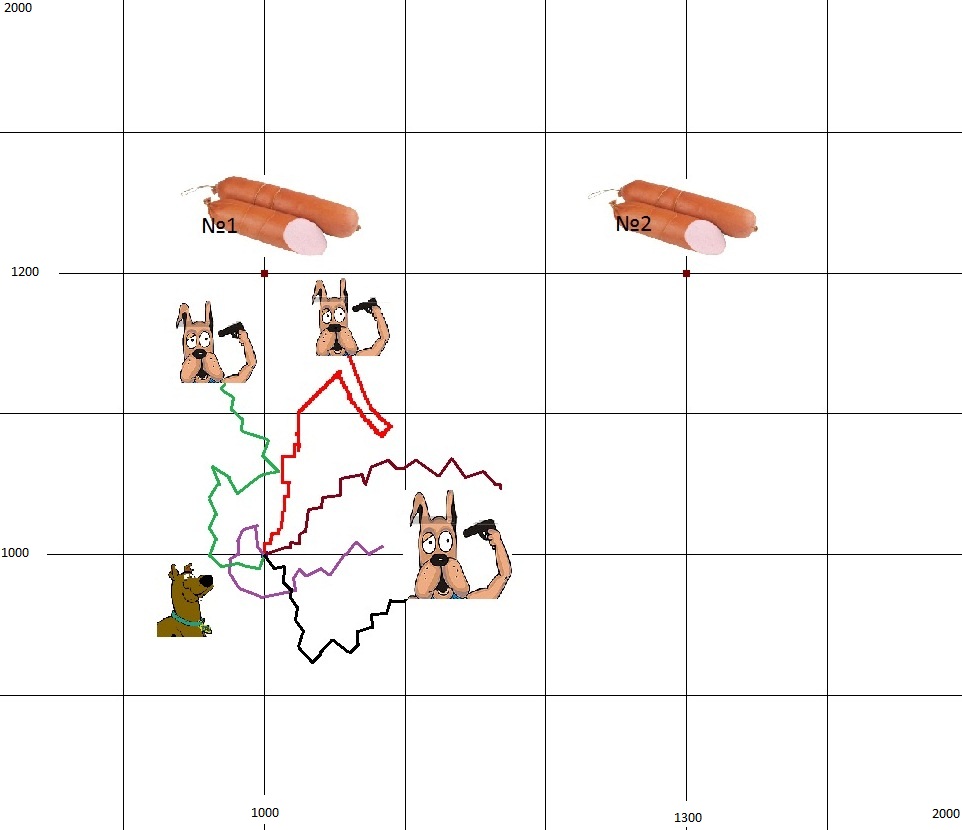
(ii) Two other examples ... By Yarmoluk Sergey (Left) & Potapchuk Sergey (Right)
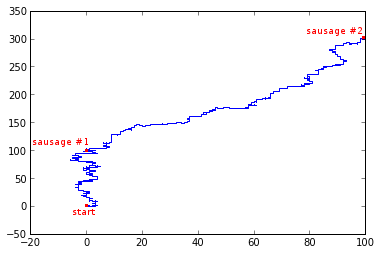
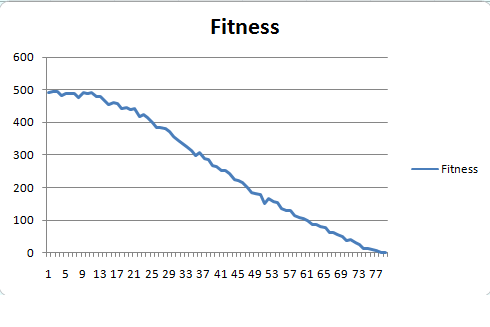
(i) A result: Generation vs Fitness (Left) and the path of the final lucky dog (Right) ... By Novik Rodion
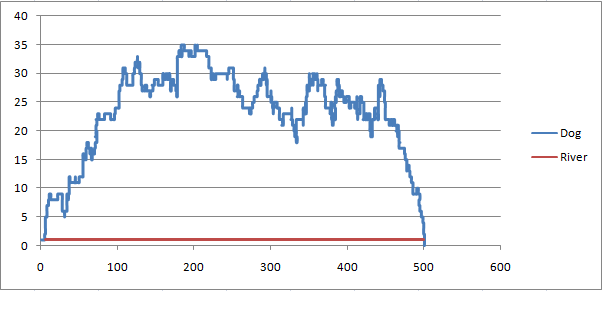
(ii) A result ... By Khomushko Olga
Even-N-Parity Problem using N-N-1 Neural Network (i) A result of N =5 ... By Romanyk Oksana
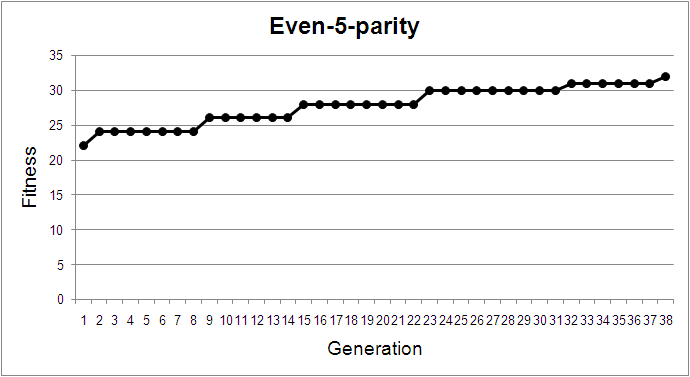
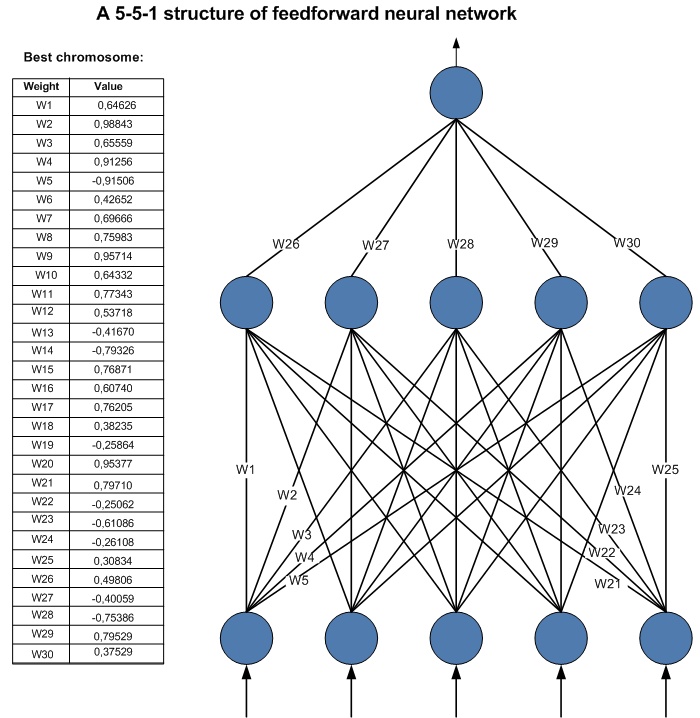
(ii) N =5, 7, 9, 11. How evolution looked? ... By Jankevitch Sergey
(iii) N =5, 7, 9, 11. How many output were correct? ... By Kutushina Tatyana
Iterated Prisnner's Dilemma (IPD) Each player has one 64-bit chromosome to follow for the next action (stragegy). Strategy is according to 6 previous actions in a row (history). Game starts with three series of randomly chosen action followed by 20 actions. Action is either 1 (corporate) and 0 (not-corporate). If (1,1) both will get 2$, if (0,0) both will get 3$, and if (1,0) player who acted "1" will get 1$ and player who acted "0" will get 5$. Fitness is the number of wins of the player who made this game with N other players one by one (Maximum=N, minimum=0).
(i) fitness vs generation (Bottom-Left), resultant stronguest strategy (Up - not yet shown), and its 12 game examples ... By Vyshinskaya Natalia
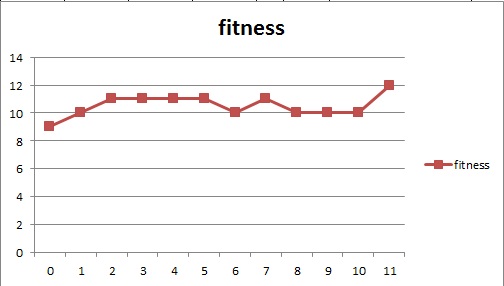
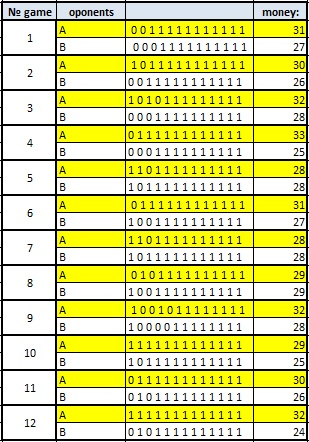
=> The strongest chromosome found after 11 generation seems to say "Always act 1." It tested with 12 matches with other chriomosoms chosen also in the last generation. The result is 9 wins and 3 ties. This result is not so dramatic. But why?
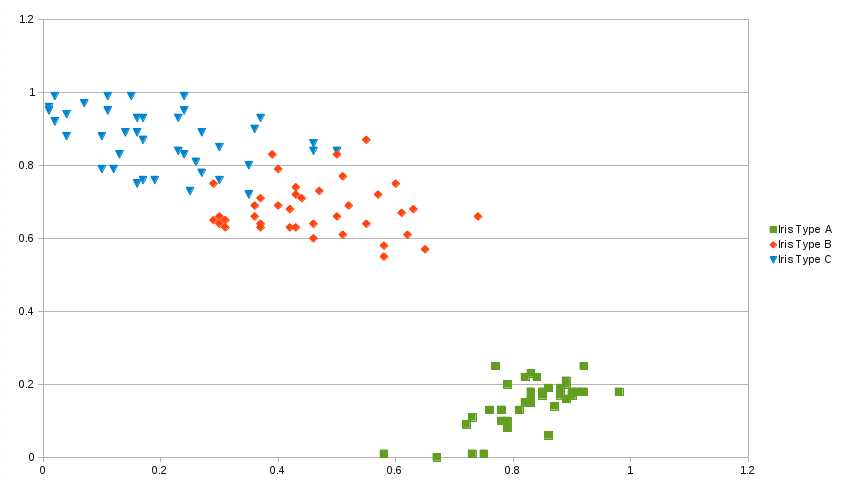
Dimension Reduction by Samon Mapping Three species of Iris flower each with 50 points ... By Doronin Nikolai
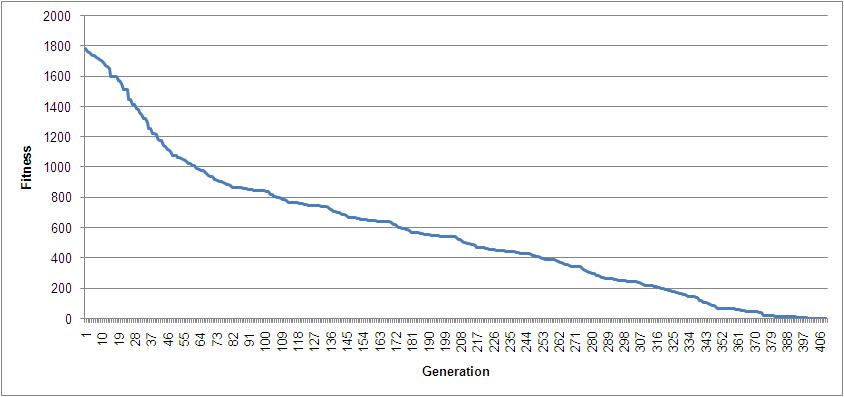
(i) One example ... By Romanyk Oksana
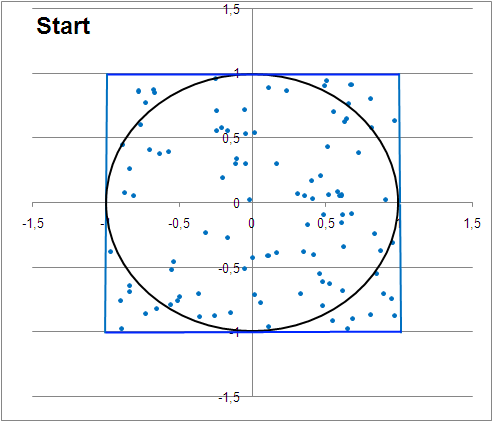
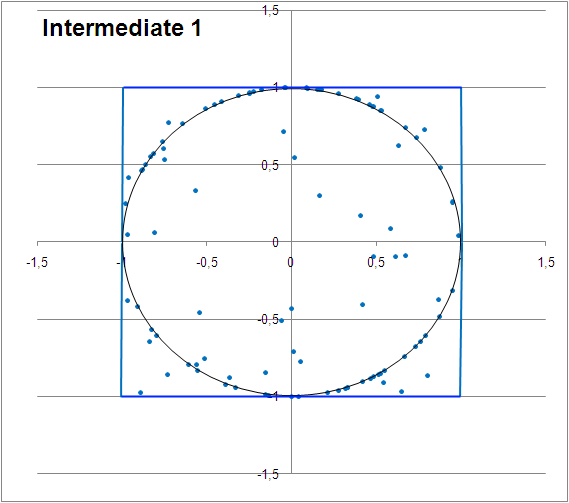
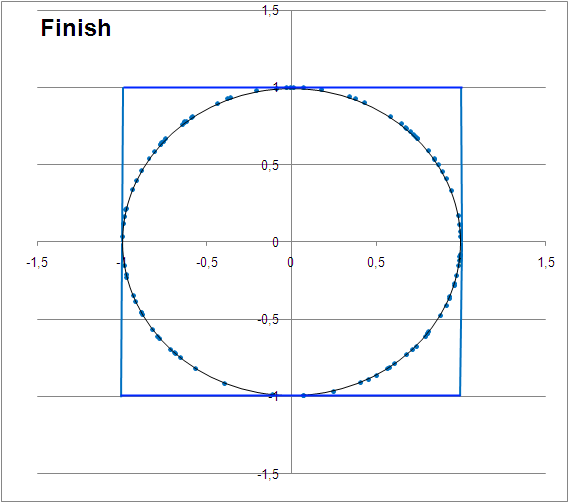
(ii) Yet another example ... By Kolamiiceva Anna
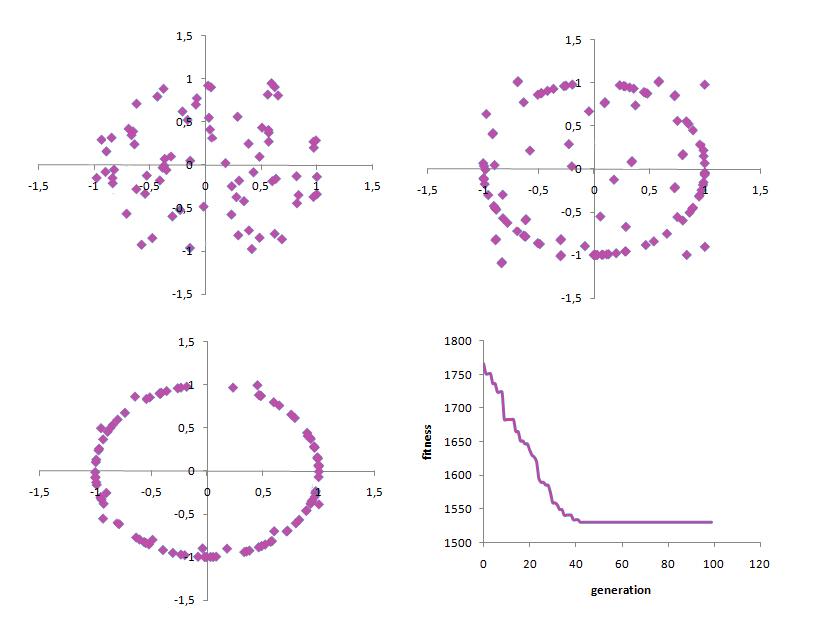
=> Good, but initial poplulation is chosen at random from lectangle, not from circle.
(iii) Example of distance matrix of 10-D (Left) and 2-D (Right) ... By Shvab Andrey
When we have multiple solutions y = sin^9(10*pi*x) ... By Potapchuk Sergey
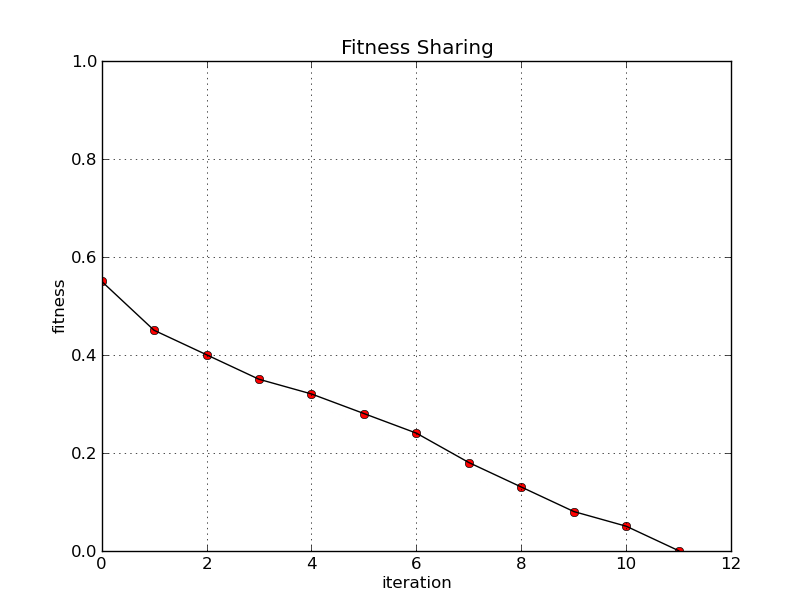
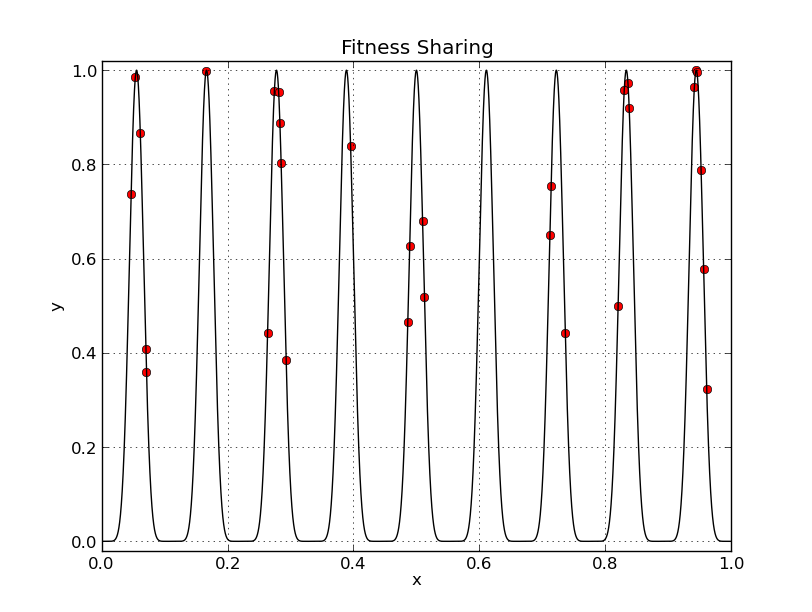
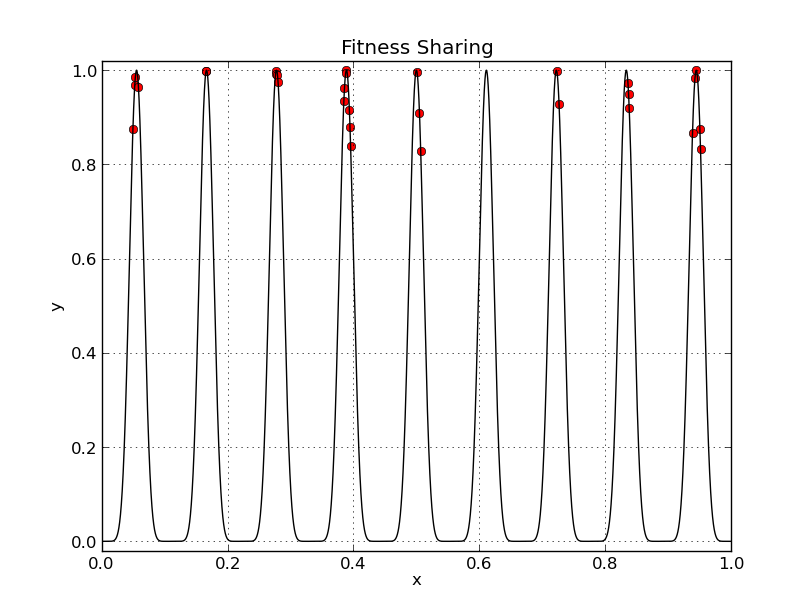
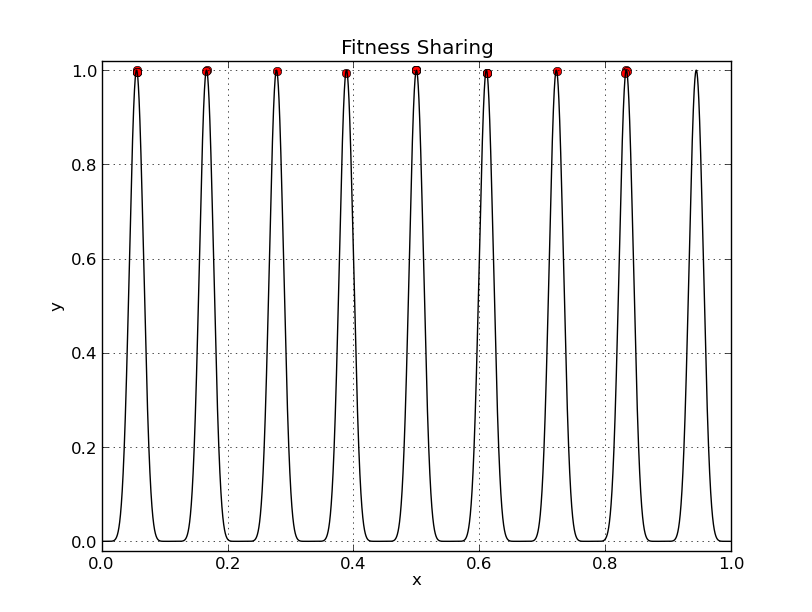
Sorting Network - What is the minimum number of comparison? (i) A minimization of comparison when 8 items are to be sorted ... By Kutushina Tatyana
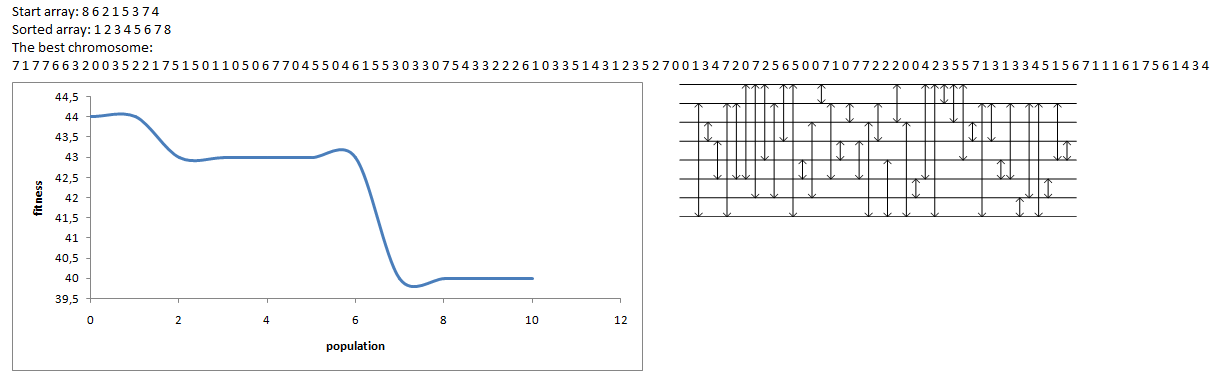
(ii) Another example ... By Klimovich Andrey
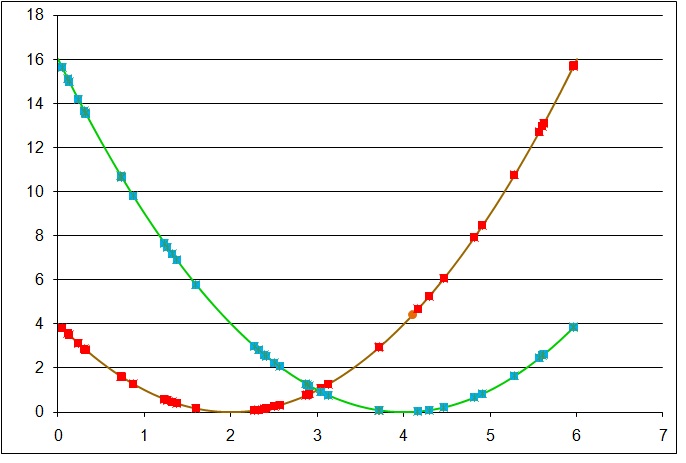
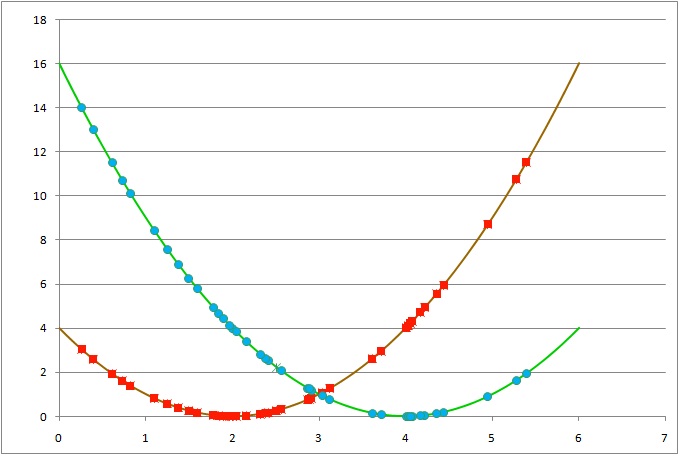
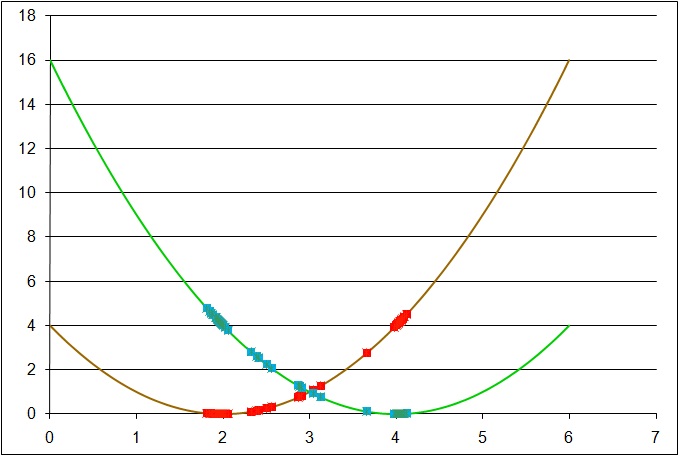
Multi Objective GA - When we have multiple fitness criteia? Seeking for non dominated (Parete optimum) solutions of y = (x-2)^2 & y=(x-4)^2 ... By Bursov Dima
