Brest State Technical University, Course "Contemporary Intelligent Information Technology (CIIT)"
From Students' Works (2013)
A dimension reduction: Sammon Mapping
Let's start with a simple experiment, not a dimension reduction though. How a set of random 100 points in 2-D space evolve to be such that all the points as close as possible to each other.
=> Chromosome is 100 pairs of (x,y) of each point, like ((3.2,5.8) (1.3,9.2) (7.6,0.3) ...... (5.4,2.6))
=> Calculate distance matrix (100 x 100) whose i-j element is distance from point i to point j. Note that the matrix is symetric and all diagonal elements are 0. Then fitness is some of those elements. The less the better.
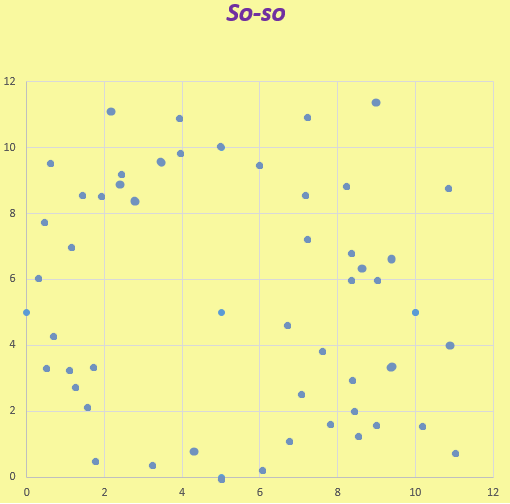
A result ... By Demchuk Kristina
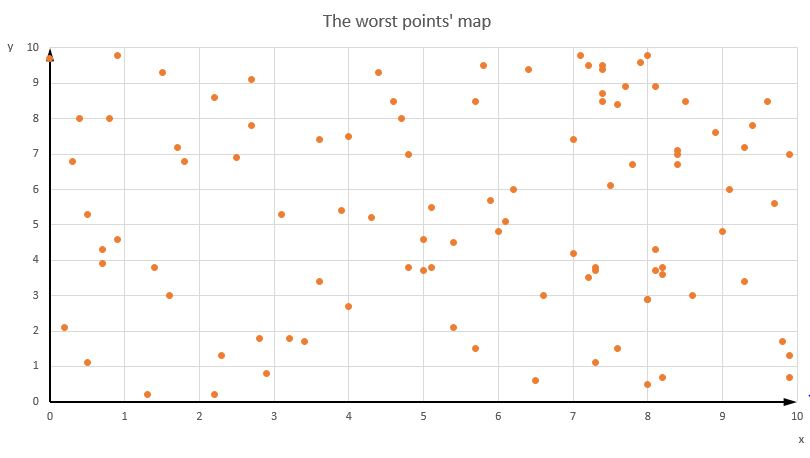
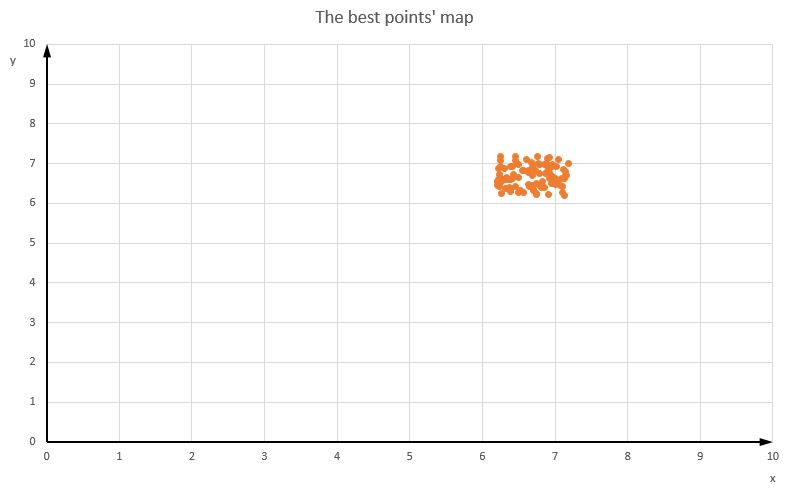
=> It looks good but I don't understand why those points converge to a rectangle-like shape, not converge to almost one point.
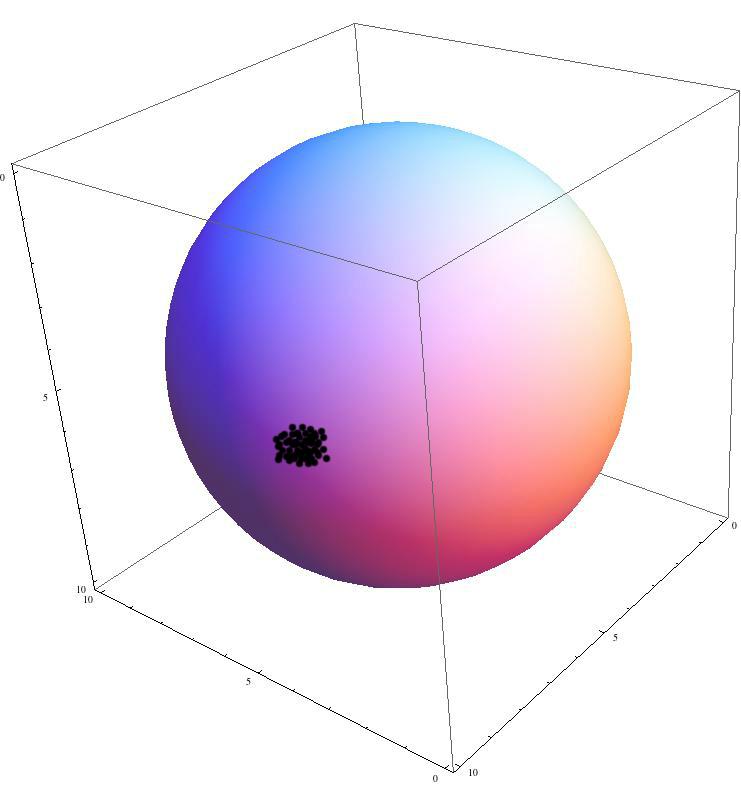
3-D version ... By Lisenkov Roman
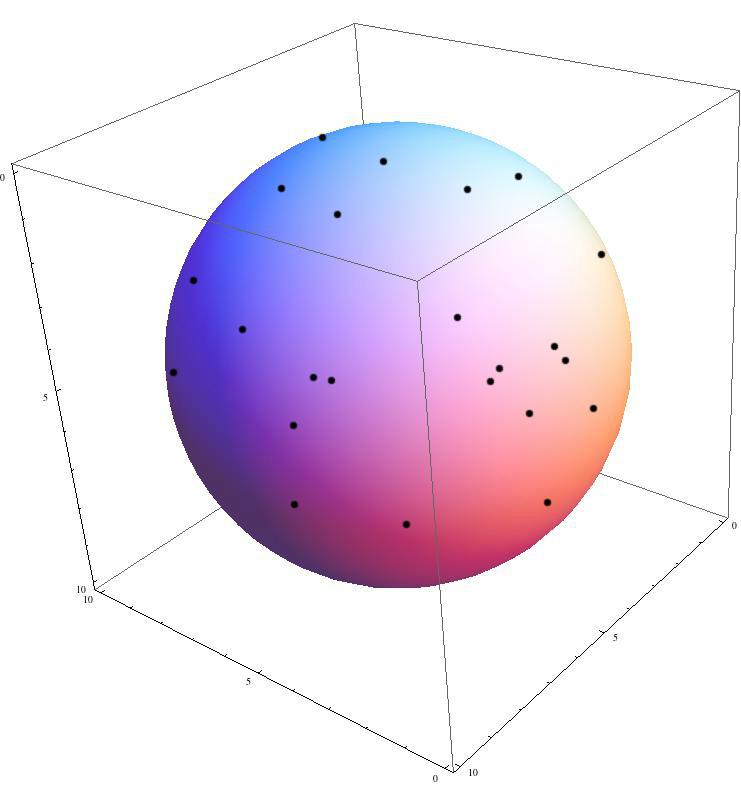
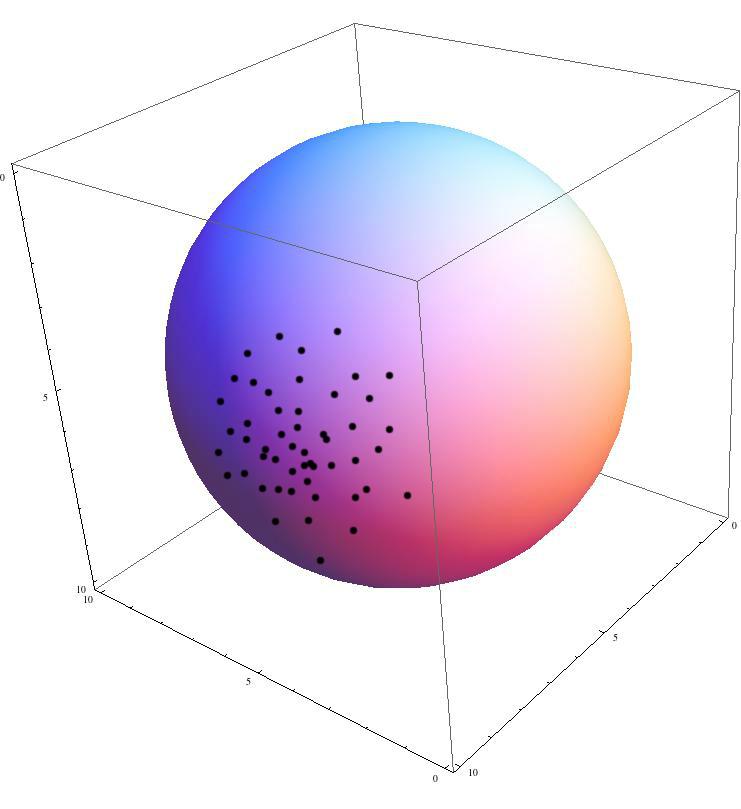
Examples of our target - 50 random points on the surface of 5-D hyperspher with its center being (5, 5, 5, 5, 5) and its radious being 5.
The equation of this 5-D hyperspere is
(X1 5)^2 + (X2 - 5)^2 + (X3 - 5)^2 + (X4 - 5)^2 + (X5 - 5)^2 = 25.
So, create X1, X2, X3, X4 at random, then calculate X5 from the equation.
(1) The 1st example ... By Vasily Brutsky
(4,23 3,49 7,2 5,4 0,86), (5,66 4,41 3,27 5,42 0,41), (4,88 1,63 3,38 4,53 1,72), (4,72 3,81 5,63 1,88 1,34), (4,98 3,58 3,34 7,75 1,44), (4,38 7,51 8,38 4,46 2,43), (5,39 5,03 2,2 2,8 1,51), (5,35 5,86 4,12 8,6 1,77), (5,43 1,18 6,49 5,4 2,2), (6,61 3,41 6,11 3,39 0,99), (7,41 2,01 3,36 2,52 3,81), (6,9 7,73 4,3 5,95 1,46), (0,74 4,52 4,52 3,25 3,18), (4,88 5,32 5,44 7,1 0,5), (4,28 2,18 8,06 2,89 3,35), (8,36 3,29 2,65 2,9 4,08), (4,72 5,19 5,15 9,64 3,17), (6,78 5,51 8,97 5,29 2,61), (3,44 8,31 3,33 3,32 2,55), (8,76 7,24 6,42 6,72 4,07), (7,03 8,42 6,45 3,34 2,92), (7,33 2,45 6,12 1,99 3,34), (5,57 7,74 3,23 6,1 1,42), (1,29 7,72 6,42 6,31 4,68), (1,11 4,43 5,57 2,83 2,88), (2,16 8,19 2,64 5,63 4,11), (1,49 6,95 6,37 5,58 2,42), (4,98 4,57 8,09 7,89 2,37), (3,87 2,78 1,64 3,24 2,9), (7,23 2,63 7,48 4,62 2,15), (2,88 7,07 4,58 6,38 1,24), (3,66 4,3 1,35 5,99 2,1), (5,52 7,74 4,04 8,86 3,82), (3,41 6,27 5,85 7,91 1,58), (1,97 4,51 5,46 5,85 1,17), (8,06 2,75 2,99 7,44 4,24), (4,94 5,08 5,64 6,34 0,23), (8,85 4,56 4,65 8,13 4,75), (6,1 2,34 8,24 3,5 3,01), (6,6 2,61 3,78 5,51 1,13), (5,44 7,65 3,45 8,27 2,83), (8,21 6,46 1,9 6,33 3,91), (5,6 3,24 1,59 3,61 2,17), (5,69 3,57 1,19 3,67 2,51), (6,53 6,79 6,84 7,39 1,78), (4,87 8,29 5,6 8,12 2,98), (5,65 5,38 9,46 3,02 4,21), (6,28 0,7 5,84 6,82 4,08), (3,43 3,99 7,92 7,17 2,12), (9,32 6,8 4,3 4,28 3,55)
(2) The 2nd example ... By Dubrovsky Alexander
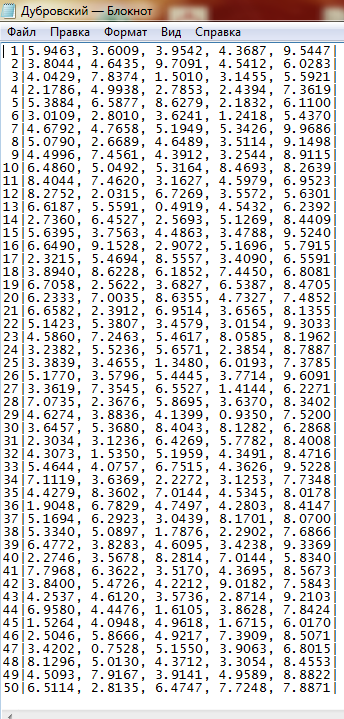
(2) The 3rd example: 10-D instead of 5-D ... By Danilchyk Raman
Sammon mapping from 50 points on the surface of 5-D sphere from the Brutsky's data above to 2-D
(1) The 1st example ... Bakunovich Dmitriy
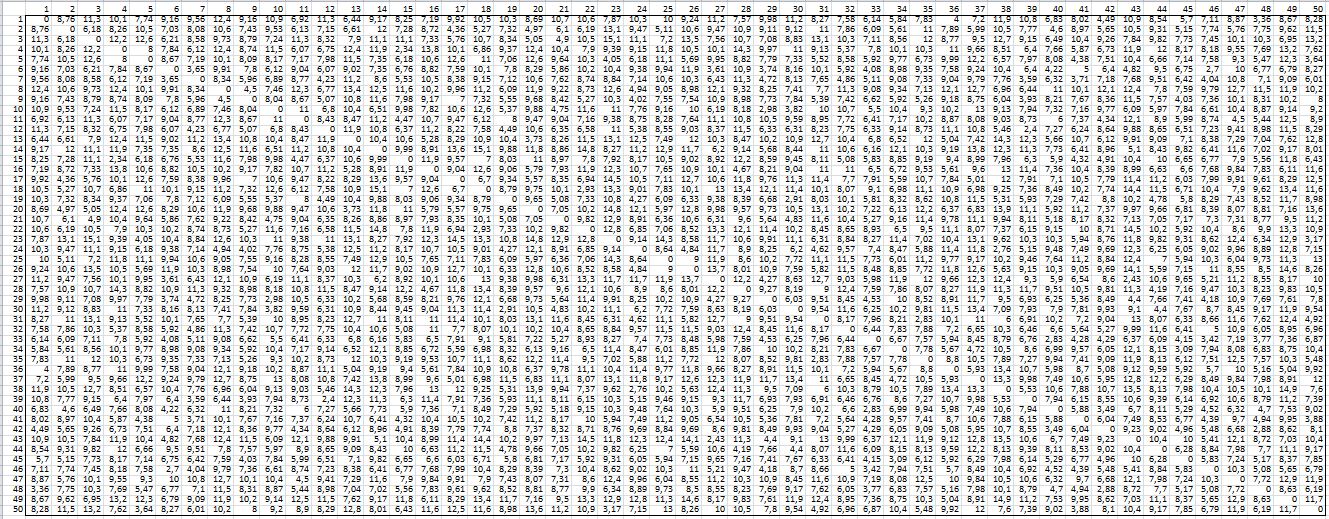
Distance Matrix of the 50 points in 5-D (Left), the one in 2-D at the start (Center), and at the goal (Right).
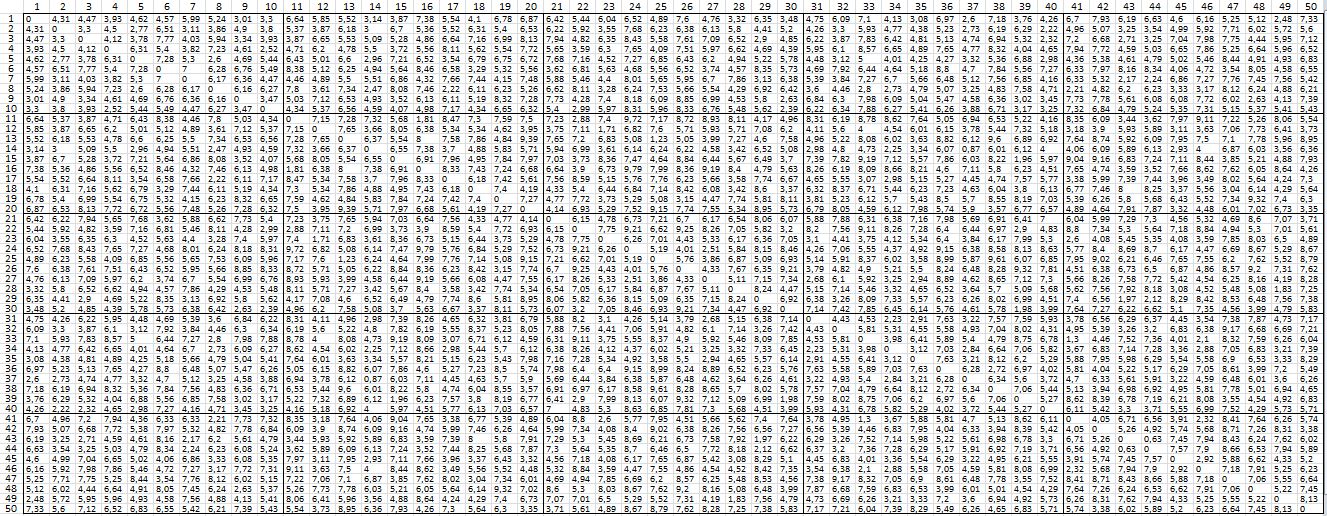
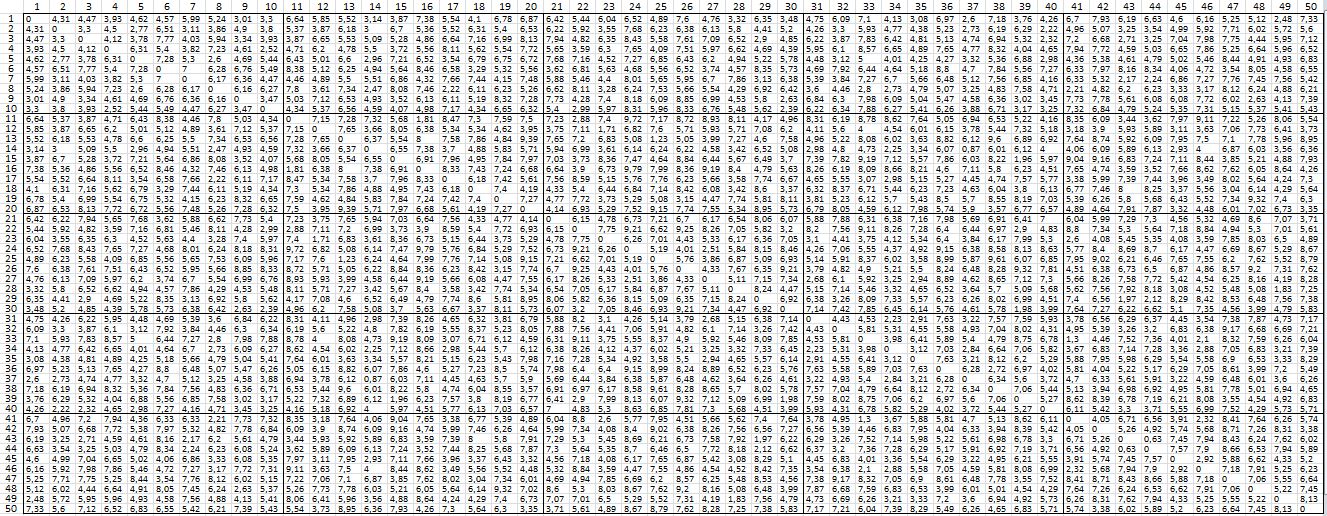
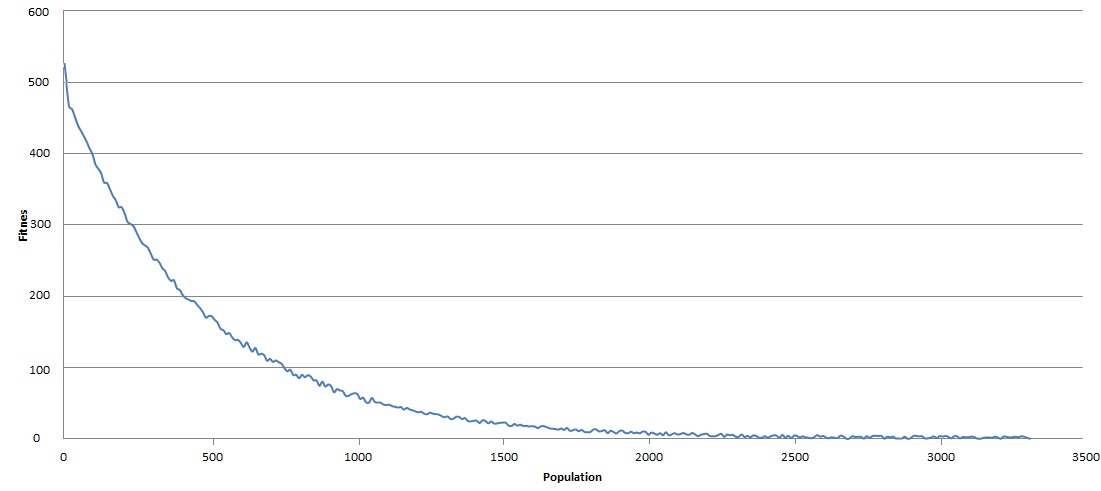
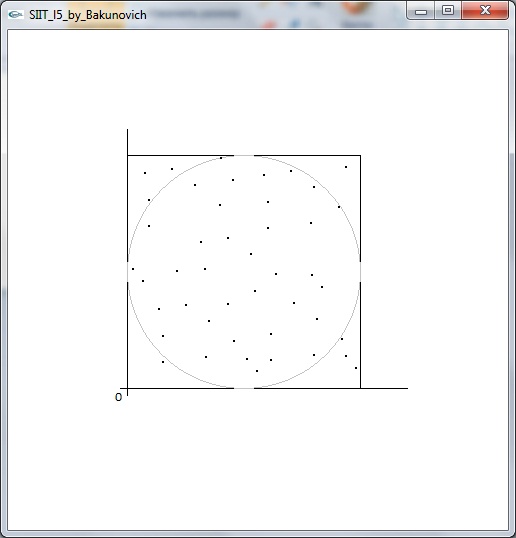
Then fitness-generation curve ((Left), 50 random points in 2-D at the start (Center), and almost perfectly mapped the final 50 points (Right)
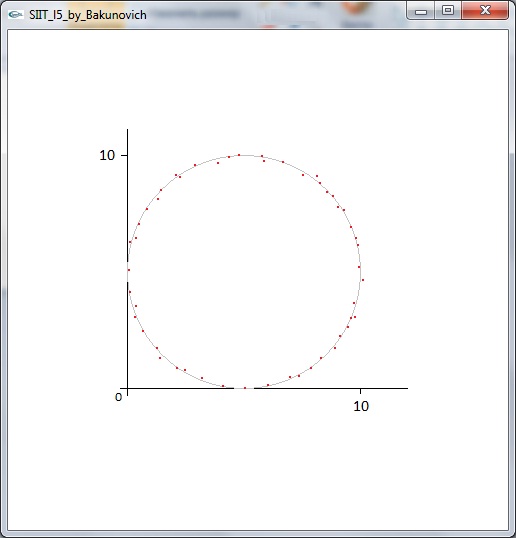
(2) The 2nd example ... By Kabachuk Roman
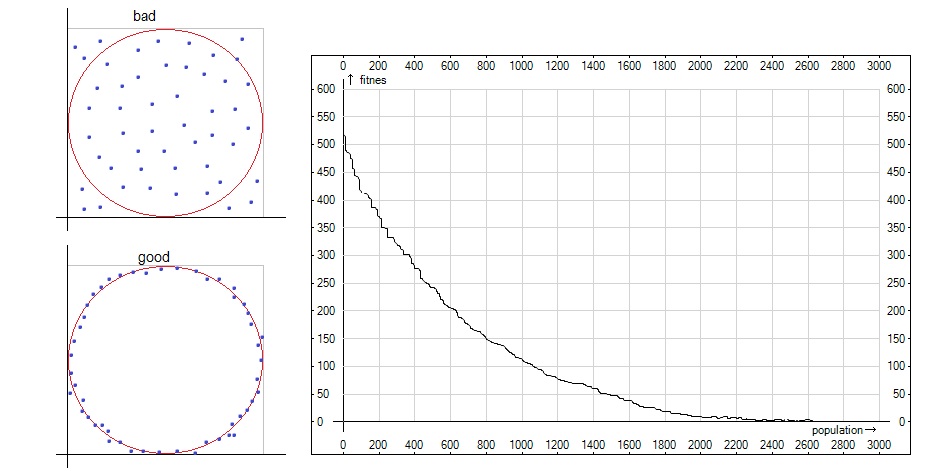
(3) An intermediate set of 50 points: Not random any more but not on a circle yet ... By Galina Bezabrazava
