For research we use Hopfield network with 49
neurons, bipolar vectors (only -1 & +1), synchronous mode, activation
function – signum, for training – method of projections (![]() ).
).
Exercise 1 (10
Patterns to be Stored). Create your own 10 patterns each of which is made up
10x10 binary pixels[1].


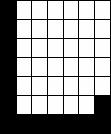




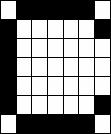


Exercise 2 (Observe
the behaviors of your Hopfield Network). Give one of your patterns to your
Hopfield Network with random weights values, and observe what will happen. Then
observe the pattern for t=1,2,…, namely, how the patterns changes as time
proceeds.
Patterns changes as time proceeds (synchronous
mode, random weights)[2]:
Step #0 – initial pattern Step #1 Step #2 – recognized pattern



Step #0 – initial pattern Step #1 Step #2 –
recognized pattern



Step #0 – initial pattern Step #1 Step #2 –
recognized pattern



Step #0 – initial pattern Step #1 Step #2 –
recognized pattern



Obvious advantage of this method is a small
number of steps which needed for pattern recognition by Hopfield network (only
2 steps).
Exercise 3 (Observe
the behaviors of your Hopfield Network Part II). Repeat the previous exercise with
the weights calculated with the above equation, instead of random values.
Patterns changes as time proceeds (synchronous mode):
Step #0 – initial pattern Step #1 Step #2 –
recognized pattern



Next patterns recognized as clear «H».
Pattern #1 Pattern #2 Pattern #3 Recognized pattern
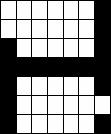
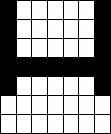
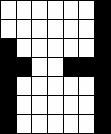

Structure of result’s listing: pattern with
noise (in) – pattern recognized with network (out). In all input patterns
amount of noisy bits is 5.



















Exercise 4 (Observe
the behaviors of your Hopfield Network Part III). Starting with 1 pattern, test
the capability of the Network by incrementing the number of noisy bits from
zero, and observe when the Network become to be chaotic. Plot this critical
number as a function of number of noise with a parameter of the number of
patterns stored.
The Hopfield Network trained by method of
projections has capacity in N-1 pattern, where N – a number of Network’s
neurons. So it’s not evident that a critical number of noisy bits as a function
depend on the number of patterns stored which more less than the number of
neurons (10 << 49).
And there is one more fact that such function
don’t depend only the number of stored patterns. For example, the position of
noisy bit also influence to pattern recognize result.
Next pattern (3 noisy bits):

had recognized as (1 noisy bit):

while the next pattern (3 noisy bits):

had recognized as (0 noisy bits):

Plot graph of the function «Noisy bits in
output pattern = g (Noisy bits in input pattern)».
As initial pattern (noisy bits=0) we have «Z».
Pixels were deleted one by one in «left-right» and «up-down» directions (fig.
1).
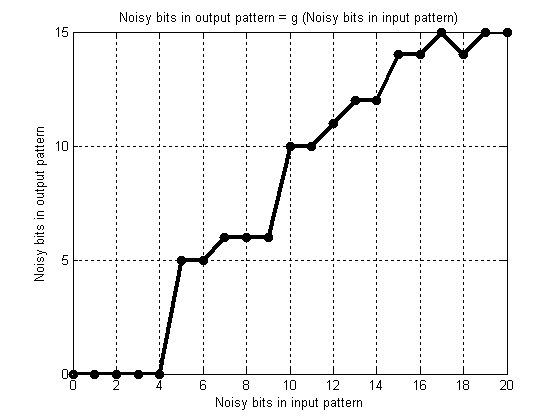
Fig. 1. Graph of the function g
Program’s listing.
All these functions are realized with Matlab,
version 7.0.0.19920 (R14).
File init.m.
function [ x, w ] = init()
%x - initial patterns
%w - Hopfield network's weights
%Initial images/patterns (see exercise #1)
%white color - (-1)
%black color - (+1)
%Initialization of the patterns
x = [
%P E
L I H
S N C
A Z
%1 row
1 1
1 -1 1
-1 1 -1 -1 1;
1 1
-1 -1 -1
1 -1 1
-1 1;
1 1
-1 1 -1
1 -1 1
-1 1;
1 1
-1 1 -1
1 -1 1
1 1;
1 1
-1 1 -1
1 -1 1
-1 1;
1 1
-1 -1 -1
1 -1 1
-1 1;
-1 1
-1 -1 1
-1 1 -1
-1 1;
%2 row
1 1
1 -1 1
1 1 1
-1 1;
-1 -1
-1 -1 -1
-1 1 -1
-1 -1;
-1 -1
-1 -1 -1
-1 -1 -1
1 -1;
-1 -1 -1 1
-1 -1 -1
-1 -1 -1;
-1 -1
-1 -1 -1
-1 -1 -1
1 -1;
-1 -1
-1 -1 -1
-1 -1 -1
-1 1;
1 -1
-1 -1 1
1 1 1
-1 -1;
%3 row
1 1
1 -1 1
1 1 1
-1 -1;
-1 -1
-1 -1 -1
-1 -1 -1
1 -1;
-1 -1
-1 -1 -1
-1 1 -1
-1 -1;
-1 -1
-1 1 -1
-1 -1 -1
-1 -1;
-1 -1
-1 -1 -1
-1 -1 -1
-1 1;
-1 -1
-1 -1 -1
-1 -1
-1 1 -1;
1 -1
-1 -1 1
-1 1 -1
-1 -1;
%4 row
1 1
1 -1 1
-1 1 1
1 -1;
-1 1
-1 -1 1
1 -1 -1
-1 -1;
-1 1
-1 -1 1
1 -1 -1
-1 -1;
-1 1 -1
1 1 1
1 -1 -1
1;
-1 1
-1 -1 1
1 -1 -1
-1 -1;
-1 -1
-1 -1 1
1 -1 -1
-1 -1;
1 -1
-1 -1 1
-1 1 -1
1 -1;
%5 row
1 1
1 -1 1
-1 1 1
1 -1;
1 -1
-1 -1 -1
-1 -1 -1
1 -1;
1 -1
-1 -1 -1
-1 -1 -1
1 1;
1 -1
-1 1 -1
-1 -1 -1
1 -1;
1 -1
-1 -1 -1
-1 1 -1
1 -1;
1 -1
-1 -1 -1
-1 -1 -1
1 -1;
-1 -1
-1 -1 1
1 1 -1
1 -1;
%6 row
1 1
1 -1 1
1 1 1
1 -1;
-1 -1
-1 -1 -1
-1 -1 -1
-1 1;
-1 -1
-1 -1 -1
-1 -1 -1
-1 -1;
-1 -1
-1 1 -1
-1 -1 -1
-1 -1;
-1 -1
-1 -1 -1
-1 -1 -1
-1 -1;
-1 -1
-1 -1 -1
-1 1 -1
-1 -1;
-1 -1
1 -1 1
1 1 1
1 1;
%7 row
1 1
1 -1 1
-1 1 -1
1 1;
-1 1
1 -1 -1
1 -1 1
-1 1;
-1 1
1 1 -1
1 -1 1
-1 1;
-1 1
1 1 -1
1 -1 1
-1 1;
-1 1
1 1 -1
1 -1 1
-1 1;
-1 1
1 -1 -1
1 -1 1
-1 1;
-1 1
1 -1 1
-1 1 -1
1 1;
];
%Initialization of the weights
w = x*inv((x')*x)*(x');
File sim.m.
function [ y, pic ] = sim( x, w )
flag = 1;
n = 49;
tmp1 = [];
tmp2 = [];
y = [];
m = 500;
k = 1;
pic = [];
l = 7;
if size(x, 1) < size(x, 2)
x = x';
end
if size(x, 1) == n
k = 1;
for i = 1:1:l
for j = 1:1:l
if x(k) == -1
pic(i, j) =
uint8(1);
else
pic(i, j) =
uint8(0);
end
k = k+1;
end
end
figure(m+1);
imshow(pic);
for i = 1:1:n
tmp2(i) = -1;
end
k = 0;
while (flag == 1) &&
(k <= m)
tmp1 = w*x;
for i = 1:1:n
if tmp1(i) > 0
y(i) = 1;
else
y(i) = -1;
end
end
if norm(y-tmp2) == 0
flag = 0;
else
tmp2 = y;
end
k = k+1;
p = 1;
for i = 1:1:l
for j = 1:1:l
if y(p) == -1
pic(i, j) =
uint8(1);
else
pic(i, j) = uint8(0);
end
p = p+1;
end
end
figure(k);
imshow(pic);
end
if k > m
disp('Can not
recognize!');
else
k = 1;
for i = 1:1:l
for j = 1:1:l
if y(k) == -1
pic(i, j) =
uint8(1);
else
pic(i, j) =
uint8(0);
end
k = k+1;
end
end
figure(m+2);
imshow(pic);
end
else
disp('Incorrect x!');
end
File randsim.m.
function [ y, pic ] = randsim( x )
flag = 1;
n = 49;
tmp1 = [];
tmp2 = [];
y = [];
m = 500;
k = 1;
pic = [];
l = 7;
if size(x, 1) < size(x, 2)
x = x';
end
w = 2*rand(n)-1;
if size(x, 1) == n
k = 1;
for i = 1:1:l
for j = 1:1:l
if x(k) == -1
pic(i, j) =
uint8(1);
else
pic(i, j) =
uint8(0);
end
k = k+1;
end
end
figure(m+1);
imshow(pic);
for i = 1:1:n
tmp2(i) = -1;
end
k = 0;
while (flag == 1) &&
(k <= m)
tmp1 = w*x;
for i = 1:1:n
if tmp1(i) > 0
y(i) = 1;
else
y(i) = -1;
end
end
if norm(y-tmp2) == 0
flag = 0;
else
tmp2 = y;
end
k = k+1;
p = 1;
for i = 1:1:l
for j = 1:1:l
if y(p) == -1
pic(i, j) =
uint8(1);
else
pic(i, j) =
uint8(0);
end
p = p+1;
end
end
figure(k);
imshow(pic);
end
if k > m
disp('Can not recognize!');
else
k = 1;
for i = 1:1:l
for j = 1:1:l
if y(k) == -1
pic(i, j) =
uint8(1);
else
pic(i, j) =
uint8(0);
end
k = k+1;
end
end
figure(m+2);
imshow(pic);
end
else
disp('Incorrect x!');
end