Parzen-Window Sample Size

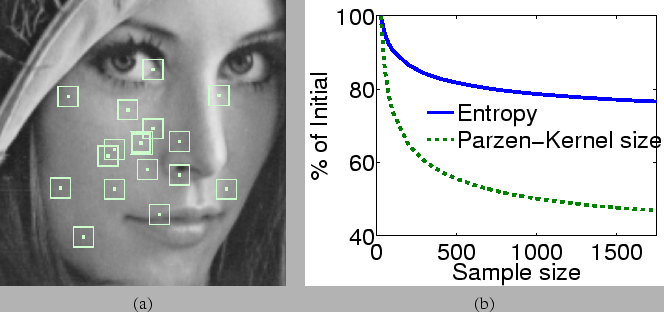
Section 3.4 described that we chose the ML (or, equivalently, minimum entropy) value of the Gaussian-kernel standard-deviation $\sigma$ . We have found that for sufficiently large sample size $\vert\mathcal{A}_t\vert$, the choice of $\sigma$ is not sensitive to the value of $\vert\mathcal{A}_t\vert$, thereby enabling us to automatically set $\vert\mathcal{A}_t\vert$ to an appropriate value before the processing begins. Figure 3.2(b) depicts this behavior. Thus, given the Markov neighborhood and the local-sampling Gaussian variance, the method chooses the critical Parzen-window kernel parameters $\sigma$ and $\vert\mathcal{A}_t\vert$ automatically in a data-driven fashion using information-theoretic metrics.

Figure: Parzen-window sampling. (a) Some pixels in $\mathcal{A}_t$ (black dots) along with the neighborhoods (squares around the dots) that form the Parzen-window sample for pixel $t$ (square with thickest edges). (b) The entropy of the Markov PDF and the optimal $\sigma$ are almost unaffected for $\vert\mathcal{A}_t\vert > 1000$. (To give smoother curves, each measurement, for a particular $\vert\mathcal{A}_t\vert$, is averaged over three different random sets $\mathcal{A}_t$).