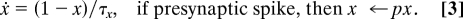|
Note:
Performing your original search, integrate-fire consciousness stdp, in
PubMed Central will retrieve 2
citations.
|
|
|
Proc Natl Acad Sci U S A.
2008 March 4;
105(9):
3593–3598.
doi:
10.1073/pnas.0712231105. |
PMCID:
PMC2265160 |
Copyright
© 2008 by The National Academy of Sciences of the USA
Neuroscience
Large-scale model of mammalian thalamocortical
systems
Eugene M. Izhikevich and
Gerald M. Edelman*
The Neurosciences Institute, 10640 John Jay Hopkins
Drive, San Diego, CA 92121
Received December 21, 2007.
|
|
Abstract
The understanding of the
structural and dynamic complexity of mammalian brains is greatly
facilitated by computer simulations. We present here a detailed
large-scale thalamocortical model based on experimental measures in
several mammalian species. The model spans three anatomical scales.
(i) It is based on global (white-matter) thalamocortical anatomy
obtained by means of diffusion tensor imaging (DTI) of a human brain.
(ii) It includes multiple thalamic nuclei and six-layered
cortical microcircuitry based on in vitro labeling and
three-dimensional reconstruction of single neurons of cat visual cortex.
(iii) It has 22 basic types of neurons with appropriate laminar
distribution of their branching dendritic trees. The model simulates one
million multicompartmental spiking neurons calibrated to reproduce known
types of responses recorded in vitro in rats. It has almost half
a billion synapses with appropriate receptor kinetics, short-term
plasticity, and long-term dendritic spike-timing-dependent synaptic
plasticity (dendritic STDP). The model exhibits behavioral regimes of
normal brain activity that were not explicitly built-in but emerged
spontaneously as the result of interactions among anatomical and dynamic
processes. We describe spontaneous activity, sensitivity to changes in
individual neurons, emergence of waves and rhythms, and functional
connectivity on different scales.
Keywords: brain models, cerebral cortex, diffusion tensor imaging,
oscillations, spike-timing-dependent synaptic
plasticity |
The last decade has seen great progress
in our understanding of brain dynamics and underlying neuronal mechanisms.
Linking these mechanisms to behavior such as perception is facilitated by
large-scale computer simulations of anatomically detailed models of the
cerebral cortex ( 1– 3). Although these models have stressed microcircuitry and
local dynamics, they have not incorporated multiple cortical regions,
corticocortical connections, and synaptic plasticity. In the present
article, we describe a large-scale model of the mammalian thalamocortical
system that includes these components. Spatiotemporal dynamics of the simulation show
that some features of normal brain activity, although not explicitly built
into the model, emerged spontaneously. The model exhibited self-sustained
activity in the absence of any external sources of input. The behavior of
the model was extremely sensitive to contributions of individual spikes:
adding or removing one spike of one neuron completely changed the state of
the entire cortex in <0.5 s. Regions of the model brain exhibited
collective waves and oscillations of local field potentials in the delta,
alpha, and beta ranges, similar to those recorded in humans ( 4). Simulated fMRI signals exhibited slow fronto-parietal
anti-phase oscillations, as seen in humans ( 5). The shape and connectivity of the model
were determined by diffusion tensor imaging (DTI) data for a human brain.
Experimental data from three species, human, cat, and rat, were
incorporated to build other details of the model. |
|
Model Structure.
|
Fig.
1.
The model's global
thalamocortical geometry and white matter anatomy was obtained by
means of diffusion tensor imaging (DTI) of a normal human brain. In
the illustration, left frontal, parietal, and a part of temporal
cortex have been cut to show a small
(more ...) |
|
Fig.
2.
Simplified diagram
of the microcircuitry of the cortical laminar structure
(Upper) and thalamic nuclei (Lower). Neuronal and
synaptic types are as indicated. Only major pathways are shows in
the figure. Complete details are provided in SI Appendix. L1-L6
(more ...) |
|
Fig.
3.
Firing patterns and
short-term synaptic plasticity. (A) Comparisons of four
representative firing patterns recorded in vitro
(Left columns) and simulated (Right columns) using
the phenomenological model (1,2). Different neuronal types have different
values
(more ...) |
For computational reasons, the density
of neurons and synapses per mm 2 of cortical surface was
necessarily reduced. Accordingly, the model neurons have fewer synapses
and less detailed dendritic trees than those of real cortical neurons.
Although we do not explicitly model subcortical structures other than the
thalamus, we do simulate brainstem neuromodulation, including the
dopaminergic reward system ( 6, 7) and the cholinergic activating system. Developmental
changes, other than activity-dependent fine-tuning of connectivity due to
dendritic STDP, are also not modeled explicitly. |
|
Macroscopic Anatomy.
Diffusion tensor imaging (DTI) data
derived from magnetic resonance imaging (MRI) of a human brain was used to
identify the coordinates of the cortical surface to allocate cell bodies
of model neurons at appropriate locations. Consequently, the model
reflects all areas of the human cortex, the folded cortical structure with
sulci and gyri. The DTI data, analyzed using the “TensorLine” algorithm
( 8, 9), formed the white matter tracts of the model, portions of
which are illustrated in ,
that connect individual neurons in one area with target neurons in other
areas. So that neuronal density approached that
of animal cortices, spatial scales were reduced by a factor of 4 (so the
model cortex diameter was 40 mm), while relative distances were preserved.
The length of the fibers determined axonal conduction delays, which were
as long as 20 ms in the model. Because DTI does not presently have
sufficient resolution, small bundles of fibers in the human brain were
inevitably missed. |
|
Microscopic Anatomy.
A summary of simulated gray matter
microcircuitry is presented in .
It is based on the detailed reconstruction studies of cat area 17 (visual
cortex) by Binzegger et al. ( 10), whose nomenclature is adapted here. Depending on the
morphology (pyramidal, spiny stellate, basket, non-basket), and the
somatic and the target layer, we distinguish eight types of excitatory
neurons [p2/3, ss4(L4), ss4(L2/3), p4, p5(L2/3), p5(L5/6), p6(L4),
p6(L5/6)] and nine types of inhibitory neurons (nb1, nb2/3, b2/3, nb4, b4,
nb5, b5, nb6, b6). See SI Appendix for a more detailed
explanation, in which we provide the matrix of intercortical connectivity
and a summary of the magnitudes of laminar axonal spread. Every area of
the model cortex had essentially the same microcircuitry as shown in . The model incorporates specific and
nonspecific nuclei of the thalamus, distinguishing two types of excitatory
thalamocortical neurons (TCs, TCn) and two types of thalamic inhibitory
interneurons (TIs, TIn) as well as the inhibitory neurons of the reticular
thalamic nucleus (RTN). Axonal arborizations and projection patterns of
thalamic neurons were all similar to those reported for LGN (see SI Appendix). |
|
Branching Dendritic Trees.
Each neuron in the model has a somatic
compartment and a number of dendritic compartments, with at least one
apical compartment per cortical layer (if the dendritic tree extends to
that cortical layer). The exact number of dendritic compartments for each
neuron was determined dynamically (see SI Appendix) during the initialization
procedure, maintaining 40 or fewer synapses per compartment. In most cases, firing of an excitatory
presynaptic neuron evoked a local EPSP in the postsynaptic dendritic
compartment of <10 mV amplitude. Such dendritic EPSPs typically result
in a submillivolt EPSP at the somatic compartment because of electrotonic
attenuation of synaptic current. Coincident firing of three or four
synapses with maximal conductances in the same compartment can result in a
local dendritic action potential (spike), which then can propagate to the
soma to evoke a spike or burst response. Similar spikes arriving at
different compartments would not be as effective in evoking a somatic
response. Conversely, somatic spikes can back-propagate to the dendritic
tree evoking dendritic spikes there. All such effects are modulated by
background excitatory and inhibitory synaptic activity. |
|
Neuronal Dynamics.
Spiking dynamics of each neuron and
each dendritic compartment are simulated by using the phenomenological
model proposed by Izhikevich ( 11), which we express here in a dimensional form ( 12):
where
C is the membrane capacitance, v is the membrane
potential (in mV), vr is the resting potential,
vt is the instantaneous threshold potential,
u is the recovery variable (the difference of all inward and
outward voltage-gated currents), I is the dendritic and synaptic
current (in pA), and a and b are parameters. When the
membrane potential reaches the peak of the spike, i.e., v >
vpeak, the model fires a spike (action potential), and
all variables are reset according to v ← c and u ← u +
d, where c and d are model parameters. Notice
that vpeak (typically ≈+50 mV) is not a threshold but
is a peak of the spike. The firing threshold in the model (as in real
neurons) is not a parameter but a dynamic property that depends on the
state of the neuron. This neuronal model differs from
conductance-based Hodgkin-Huxley-type models ( 13). Instead of reproducing all of the ionic currents, the
model was designed to reproduce firing responses; compare in
vitro recordings and simulations in A. Different neuronal types were given
different values of the parameters in Eqs. 1 and 2; see SI Appendix. Using the nomenclature of
Connors and Gutnick ( 14), the excitatory neurons are of RS (regular spiking)
type, although some of them also exhibit burst firings evoked by dendritic
stimulation; non-basket interneurons in layer 1 (nb1) are of LS type [late
spiking ( 15)]; non-basket cells in the other layers, which
morphologically include double-bouquet cells, neurogliaform cells, and
Martinotti cells, are of LTS (low-threshold spiking) type; all basket
cells are of FS (fast spiking) type; see . |
|
Short-Term Synaptic Plasticity.
In the model, the synaptic conductance
(strength) of each synapse can be scaled down (depression) or up
(facilitation) on a short time scale (hundreds of milliseconds; see e.g.,
ref. 16) by a scalar factor x. To achieve computational
efficiency, this scalar factor, different for each synapse, is modeled by
the following one-dimensional equation
x
tends to recover to the equilibrium value x = 1 with the time
constant τ x, and it is reset by each spike of the
presynaptic cell to the new value px. The parameter p
< 1 decreases x and results in short-term synaptic depression,
whereas p > 1 results in short-term synaptic facilitation, as
we illustrate in B.
Different synaptic types have different values of p and
τ x, provided in SI Appendix. The total synaptic current at each
compartment is the sum of AMPA, NMDA, GABA A and
GABA B currents with standard kinetics (see SI Appendix). |
|
Dendritic STDP.
The long-term change of conductance
(weight) of each synapse in the model is simulated according to
spike-timing-dependent plasticity (STDP): The synapse is potentiated or
depressed depending on the order of firing of the presynaptic neuron and
the corresponding (dendritic) compartment of the postsynaptic neuron ( 17– 20). We use equations in the form provided by Izhikevich ( 21) so that the synaptic change due to the dendritic STDP
develops slowly with time with a rate modulated by dopamine. Because dendritic compartments can
generate spikes independently from the soma, synapses could be potentiated
or depressed even in the absence of spiking of the postsynaptic cell. All
GABAergic synapses in the model are nonplastic. |
|
Computer Simulation.
The program simulating the model
is written in C programming language with MPI and it is run on a Beowulf
cluster of 60 3GHz processors with 1.5 GB of RAM each. Most of the
simulations were performed with one million neurons, tens of millions of
neuronal compartments, and almost half a billion synapses. It takes ≈10
min on the cluster to initialize the model, and one minute to compute one
second of simulated data using a sub-millisecond time
step. |
|
Results of Simulations
Spontaneous Activity.
If there are no spikes fired by the
network at the beginning of each simulation, there are no synaptic inputs,
and no new spikes, so the network remains completely quiet. To jump-start
the network, we introduced a few seed (random) spikes at time t =
0. Regardless of the number of seed spikes, the initial strength of
synaptic connections, or the size of the network (we tested up to 10
million neurons), the network activity died out during the first second,
as we illustrate in .
|
Fig.
4.
Spontaneous
activity in the model. Main graph: Activity (shown as mean firing
rate in the network) dies out within the first few seconds of
simulation regardless of the number of seed spikes introduced at the
beginning of the simulation. (Inset) The model
(more ...) |
One way to avoid the silent state of a spiking
network is to introduce spontaneous synaptic release, called miniature
postsynaptic potentials, mPSPs or “minis.” Such “minis,” observed both
in vitro and in vivo, are thought to feed neurons with a
tonic level of random input necessary to prevent the silent state ( 22, 23). During the period of the first 30 min of model time
(the first 1,800 s in the Inset of )
we simulated one spontaneous (Poissonian) synaptic release per synapse per
second and let synaptic plasticity modify the ongoing connectivity. If the
minis are turned off during this time, the activity would subside, but the
longer they are made to persist, the longer the activity lingers
subsequently. From our previous studies ( 24, 25) we know that STDP favors synaptic connectivity that
results in polychronous activity (i.e., time-locked but not synchronous
activity) that can reverberate through the network. Accordingly, turning
off minis at t = 1,800 s ()
did not silence the network. STDP had fine-tuned the synaptic connectivity
in such a way as to allow enough interneuronal action potentials to
maintain the global activity. (The network required >10,000 neurons to
exhibit this property). We ran the model for the next 30 min with “minis”
off (i.e., in a noiseless regime) and then used the final state at the end
of this 1-h transient period as the initial state for most of the
subsequent simulations.
Each Neuron Matters.
Unlike the real brain, where there are
many sources of sensory input and neuronal noise, the model exhibited
self-sustained activity autonomously in a noiseless environment. To
investigate whether the activity is chaotic, we tested for the major
hallmark of chaos — the sensitivity of the system to a small perturbation
of initial conditions, i.e., the “butterfly effect”: Can one spike make a
difference? That is, can the state of the entire activity pattern be
changed by a firing of a single neuron?
In we
show two traces of total electrical activity (the sum of local-field
potentials at every cortical location; see SI Appendix), starting from the same
initial conditions with the only difference being an extra spike of one
pyramidal neuron in layer 2/3 of the frontal cortex (manually introduced).
Initially, the traces look similar, but after just a few hundred
milliseconds, they diverge and result in completely different global
activity patterns.
|
Fig.
5.
Sensitivity of the
model to the addition of a single spike: two simulations starting
from the same initial condition, except for a single spike, diverge
(Upper) within half a second. (Lower) Shown is the
difference of two spike rasters corresponding to
(more ...) |
In Lower,
we show the difference in the spike rastergrams. As one can see, the extra
spike triggered an avalanche of extra spikes (blue dots) or missed spikes
(red dots) that eventually spread over the entire network and changed the
activity of every neuron.
The same effect was seen if we removed a
spike in the initial conditions. We did not find any significant
difference in the location or type of neuron whose spike was added or
removed; on average, it took 400 ms for the perturbed activity trace to
diverge one standard deviation from the unperturbed one. The divergence
became stronger (faster) as the size of the network increased, although we
did not explore this dependence on the size in detail. Similarly, the
network was sensitive to the addition of a single somatic EPSP, but it
took more time for the perturbation to propagate through the network and
often an extra EPSP had no effect on the perturbed neuron or the
network.
Brain Rhythms and Waves.
Firings of individual pyramidal and
non-basket interneurons in the model look Poissonian during self-sustained
spontaneous activity, typically two to three spikes per second. Mean
firing rates of basket cells, which are of FS type, were 7 Hz in layer 2/3
and 4, >20 Hz in layer 5 with fluctuations exceeding 60 Hz, and 8 Hz in
layer 6. These cells often had 20- to 25-ms interspike intervals and
generated strong local gamma rhythms (40–50 Hz), seen as fast propagating
waves in SI Movie 1. However, these rhythms had different
phases at different locations. When averaged over a centimeter-size area,
they canceled each other and were hardly seen in the power-spectrum of the
global electrical activity, consistent with the common experimental
observations that gamma rhythms are weaker in EEG and MEG recordings than
in LFPs and intracranial EEGs ( 4). Although not explicitly built into any type of
neurons, prominent low-frequency activity arose in the entire network ().
Its predominant frequencies were in the delta (1–3 Hz) and alpha (≈10 Hz)
ranges. The former is typical during mammalian sleep state and the latter
during human cortical idling ( 27). It is known ( 11, 25, 26) that simple models of spiking networks can self-organize
to exhibit collective delta-, alpha-, and gamma-frequency rhythms. What is
remarkable here is that the power spectra at different cortical locations
show different predominant rhythms, e.g., strong beta rhythm (≈20 Hz) in
regions corresponding to motor and somatosensory areas, even though the
cortical microcircuitry at all locations in the model is the same. Thus,
the diversity of rhythms in different areas in the model must come largely
from differences in the white-matter connectivity between and among
cortical areas. Another striking feature of the model,
illustrated in ,
is that the oscillatory activity was not uniform, but consisted of
multiple propagating waves of excitation that spontaneously appeared and
disappeared at various locations of the cortex. The waves had a spatial
extent of up to a centimeter and a speed of ≈0.1 m/s. These measures are
similar to propagating neocortical waves observed in vitro ( 28) and in vivo in visual cortex of anesthetized
rats ( 29). They are slower than those in vivo in primary
motor and dorsal premotor cortices of monkeys ( 30) and in turtle visual cortex ( 31).
|
Fig.
6.
Propagating waves
in the model. Red (black) dots are spikes of excitatory (inhibitory)
neurons. The right hemisphere is transparent to expose the waves
inside the cortex (snapshots are from SI Movie
2). |
Functional Connectivity.
As suggested by studies of human
subjects ( 5), we can analyze the resting state correlations of the
simulated signals corresponding to fMRI (BOLD signals) on the slow time
scales of minutes. Following Fox et al. ( 5), we collect signals (see SI Appendix) at each voxel of the
cortical surface, low-pass filter them between 0.1 and 0.01 Hz, and then
correlate the results with a seed region corresponding to posterior
cingulate. Regions positively and negatively correlated with the seed
region are depicted in red and blue, respectively, in .
Our results resemble those seen in experimental brain studies of human ( 5) and theoretical studies ( 32), indicating that the resting state of the mammalian
brain on this scale consists of multiple anticorrelated functional
clusters.
|
Fig.
7.
Intrinsic
correlations of fMRI signal between the seed cortical region in a
location corresponding to posterior cingulate [data not shown; see
Fox et al. (5)] and other regions in the model brain. Red (blue)
voxels correspond to positive (negative) correlations
(more ...) |
|
|
Discussion
One way to deepen our understanding of
how synaptic and neuronal processes interact to produce the collective
behavior of the brain is to develop large-scale, anatomically detailed
models of the mammalian brain. We started with the thalamocortical system
because it is necessary for human consciousness. Currently, we are at the
stage of calibrating and further validating the model by determining to
what extent its activity is similar to that recorded in the mammalian
cortex after receipt of various input signals.
Even in the absence of external input, the
distribution of firing rates among various types of neurons is similar to
that recorded in vivo: pyramidal neurons fire just a few spikes
per second with the lowest firing rate observed in layer 2/3, whereas
basket cells fire tens of spikes per second with the highest firing rate
in layer 5 ( 33). Individual neurons exhibit somatic and dendritic
spikes, forward- and back-propagation of spikes along the dendritic trees,
and spike-timing-dependent plasticity that is coupled to the dendritic
compartments rather than to the somatic spikes. The model spontaneously
generated rhythms and propagating waves ()
that had frequency distributions, spatial extents, and propagation
velocities similar to those observed in mammalian in vivo
recordings. In a fashion similar to human data, the simulated fMRI signal
exhibited slow oscillations with multiple anticorrelated functional
clusters (). The computer model allowed us to perform
experiments that are impossible (physically or ethically) to carry out
with animals. For example, we put the model into the noiseless regime to
demonstrate that it can produce self-sustained autonomous activity. We
perturbed a single spike ( 34, 35) in this regime (out of millions) and showed that the
network completely reorganized its firing activity within half a second.
It is not clear, however, how to interpret this sensitivity in response to
perturbations ().
On one hand, one could say that this sensitivity indicates that only
firing patterns in a statistical sense should be considered, and
individual spikes are too volatile. On the other hand, one could say that
this result demonstrates that every spike of every neuron counts in
shaping the state of the brain, and hence the details of the behavior, at
any particular moment. This conclusion would be consistent with the
experimental observations that microstimulation of a single tactile
afferent is detectable in human subjects ( 36), and that microstimulation of single neurons in
somatosensory cortex of rats affects behavioral responses in detection
tasks ( 37). After development of a detailed, more
complete brain model, one may simulate the effect of structural
perturbations, such as lesions, strokes, and tumors, on the global
dynamics, and compare the results with animal or human EEG/MEG data. By
using DTI of patients with Alzheimer's disease, Parkinson's disease, or
other neurological and psychiatric disorders, one may investigate how the
connectivity alone modifies brain dynamics. Changing the neuronal
parameters to simulate the effect of various pharmacological agents, one
may study the effect of drugs (including addictive drugs) on the dynamics
of the model to aid design of new therapeutic strategies against
neurological disorders. By simulating the effect of cholinergic modulatory
systems, one may induce sleep oscillations into the model and study the
dynamics of the sleep state and its effect on synaptic plasticity,
learning, and memory. Knowing the state of every neuron and every synapse
in such a model, one may analyze the mechanisms involved in neural
computations with a view toward development of novel computational
paradigms based on how the brain works. Finally, by reproducing the global
anatomy of the human thalamocortical system, one may eventually test
various hypotheses on how discriminatory perception and consciousness
arise. |
|
|
|
ACKNOWLEDGMENTS.
Data files of cortical microcircuitry were kindly
provided by Tom Binzegger, Rodney J. Douglas, and Kevan A. C. Martin (Eth
Zurich, Zurich, Switzerland). The simulations were performed by using two
MRI DTI data files, one of the brain of the first author (E.M.I.) and the
other provided by Gordon Kindlmann (Scientific Computing and Imaging
Institute, University of Utah), and Andrew Alexander [W. M. Keck
Laboratory for Functional Brain Imaging and Behavior, University of
Wisconsin-Madison ( http://www.pubmedcentral.nih.gov/redirect3.cgi?&&auth=0pizRpgkwQvhMBAPFMOgD1QHH3fpWLyMoQCgHr5oY&reftype=extlink&article-id=2265160&issue-id=162169&journal-id=2&FROM=Article%7CBody&TO=External%7CLink%7CURI&rendering-type=normal&&http://www.sci.utah.edu/gk/DTI-data/)].
Jeff Krichmar, Botond Szatmary, Douglas Nitz, and Niraj Desai provided
useful comments. The authors are especially grateful to Dr. Joe Gally, who
suggested many important improvements to the manuscript. This work was
supported by the Neurosciences Research Foundation and by National Science
Foundation Grant CCF-0523156. |
|
|
|
References
1.
Lumer ED, Edelman GM, Tononi G. Neural dynamics in a
model of the thalamocortical system. I. Layers, loops and the emergence of
fast synchronous rhythms. Cereb Cortex.
1997;7:207–227. [PubMed]
2.
Lumer ED, Edelman GM, Tononi G. Neural dynamics in a
model of the thalamocortical system. II. The role of neural synchrony
tested through perturbations of spike timing. Cereb Cortex. 1997;7:228–236. [PubMed]
3.
Markram H. The blue brain project. Nat Rev Neurosci. 2006;7:153–160. [PubMed]
4.
Nunez PL, Srinivasan R. Electric Fields of the Brain: The Neurophysics of
EEG. 2nd Ed. New York: Oxford Univ Press; 2006.
5.
Fox MD, et al. The human brain is intrinsically
organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci USA. 2005;102:9673–9678. [PubMed]
6.
Schultz W. Reward. Scholarpedia. 2007;2:1652.
7.
Schultz W. Reward signals. Scholarpedia. 2007;2:2184.
8.
Weinstein D, Kindlmann G, Lundberg E. Tensorlines:
Advection-diffusion based propagation through diffusion tensor fields..
Proceedings of the IEEE Conference on Visualization '99: Celebrating Ten
Years; Los Alamitos, CA: IEEE Computer Society Press; 1999. pp.
249–253.
9.
Mori S, van Zijl PCM. Fiber tracking: Principles and
strategies–a technical review. NRM Biomed.
2002;15:468–480.
10.
Binzegger T, Douglas RJ, Martin KAC. A quantitative
map of the circuit of cat primary visual cortex. J Neurosci. 2004;24:8441–8453. [PubMed]
11.
Izhikevich EM. Simple model of spiking neurons.
IEEE Trans Neural Netw. 2003;14:1569–1572. [PubMed]
12.
Izhikevich EM. Dynamical
Systems in Neuroscience: The Geometry of Excitability and Bursting.
Cambridge, MA: MIT Press; 2007.
13.
Skinner FK. Conductance-based models. Scholarpedia. 2006;1:1408.
14.
Connors BW, Gutnick MJ. Intrinsic firing patterns of
diverse neocortical neurons. Trends
Neurosci. 1990;13:99–104. [PubMed]
15.
Chu Z, Galarreta M, Hestrin S. Synaptic interactions
of late-spiking neocortical neurons in layer 1. J Neurosci. 2003;23:96–1002. [PubMed]
16.
Beierlein M, Gibson JR, Connors BW. Two dynamically
distinct inhibitory networks in layer 4 of the neocortex. J Neurophysiol. 2003;90:2987–3000. [PubMed]
17.
Levy WB, Steward O. Temporal contiguity requirements
for long-term associative potentiation/depression in the hippocampus.
Neuroscience. 1983;8:791–797. [PubMed]
18.
Gerstner W, Kempter R, van Hemmen JL, Wagner H. A
neuronal learning rule for sub-millisecond temporal coding. Nature. 1996;383:76–78. [PubMed]
19.
Markram H, Lubke J, Frotscher M, Sakmann B. Regulation
of synaptic efficacy by coincidence of postsynaptic APs and EPSPs.
Science. 1997;275:213–215. [PubMed]
20.
Bi GQ, Poo MM. Synaptic modifications in cultured
hippocampal neurons: Dependence on spike timing, synaptic strength, and
postsynaptic cell type. J Neurosci.
1998;18:10464–10472. [PubMed]
21.
Izhikevich EM. Solving the distal reward problem
through linkage of STDP and dopamine signaling. Cereb Cortex. 2007;17:2443–2452. [PubMed]
22.
Timofeev I, Grenier F, Bazhenov M, Seijowski TJ,
Steriade M. Origin and slow cortical oscillations in deafferented cortical
slabs. Cereb Cortex. 2000;10:1185–1199. [PubMed]
23.
Muresan RC, Savin C. Resonance or Integration?
Self-sustained dynamics and excitability of neural microcircuits.
J Neurophysiol. 2007;97:1911–1930. [PubMed]
24.
Izhikevich EM, Gally JA, Edelman GM. Spike-timing
dynamics of neuronal groups. Cereb Cortex.
2004;14:933–944. [PubMed]
25.
Izhikevich EM. Polychronization: Computation with
spikes. Neural Comput. 2006;18:245–282. [PubMed]
26.
Ananthanarayanan R, Modha DS. Anatomy of a Cortical
Simulator,. Supercomputing 07: Proceedings of the ACM/IEEE SC2007
Conference on High Performance Networking and Computing; New York, NY:
Association for Computing Machinery; 2007.
27.
Bazhenov M, Timofeev I. Thalamocortical oscillations.
Scholarpedia. 2006;1:1319.
28.
Bao W, Wu J-Y. Propagating wave and irregular
dynamics: Spatiotemporal patterns of cholinergic theta oscillations in
neocortex in vitro. J Neurophysiol.
2003;90:333–341. [PubMed]
29.
Xu W, Huang X, Takagaki K, Wu J-Y. Compression and
reflection of visually evoked cortical waves. Neuron. 2007;55:119–129. [PubMed]
30.
Rubino D, Robbins KA, Hatsopoloulos NG. Propagating
waves mediate information transfer in the motor cortex. Nat Neurosci. 2006;9:1549–1557. [PubMed]
31.
Prechtl JC, Cohen LB, Pesaran B, Mitra PP, Kleinfeld
D. Visual stimuli induce waves of electrical activity in turtle cortex.
Proc Natl Acad Sci USA. 1997;94:7621–7626. [PubMed]
32.
Honey CJ, Kotter R, Breakspear M, Sporns O. Network
structure of cerebral cortex shapes functional connectivity on multiple
time scales. Proc Natl Acad Sci USA.
2007;104:10240–10245. [PubMed]
33.
Swadlow HA. Efferent neurons and suspected
interneurons in motor cortex of the awake rabbit: Axonal properties,
sensory receptive fields, and subthreshold synaptic inputs. J Neurophysiol. 1994;71:437–453. [PubMed]
34.
Latham PE, Roth A, Hausser M, London M. Requiem for
the spike? Soc Neurosci Abstr.
2006;32:432.12.
35.
Banerjee A. On the sensitive dependence on initial
conditions of the dynamics of networks of spiking neurons. J comput Neurosci. 2006;20:321–348. [PubMed]
36.
Vallbo ÅB, Olsson KÅ, Westberg K-G, Clark FJ.
Microstimulation of single tactile afferents from the human hand: Sensory
attributes related to unit type and properties of receptive fields.
Brain. 1984;107:727–749. [PubMed]
37.
Houweling AR, Brecht M. Behavioural report of single
neuron stimulation in somatosensory cortex. Nature. 2008;451:65–68. [PubMed] |
|
|



 This article has been
This article has been  Term
Synaptic Plasticity.
Term
Synaptic Plasticity.