Maximize the distance a Jeep can penetrate into the desert using a given quantity of fuel. The Jeep is allowed to go forward, unload some fuel, and then return to its base using the fuel remaining in its tank. At its base, it may refuel and set out again. When it reaches fuel it has previously stored, it may then use it to partially fill its tank. This problem is also called the exploration problem (Ball and Coxeter 1987).
Given 
(with
) drums
of fuel at the edge of the desert and a Jeep capable of holding one drum
(and storing fuel in containers along the way), the maximum one-way
distance which can be traveled (assuming the Jeep travels one unit of
distance per drum of fuel expended) is
 |
 |
 |
|
|
 |
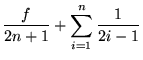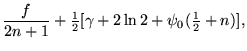where
is the
Euler-Mascheroni
constant and 
the polygamma
function.
For example, the farthest a Jeep with n = 1 drum can travel is
obviously 1 unit. However, with n = 2 drums of gas, the maximum
distance is achieved by filling up the Jeep's tank with the first drum,
traveling 1/3 of a unit, storing 1/3 of a drum of fuel there, and then
returning to base with the remaining 1/3 of a tank. At the base, the tank
is filled with the second drum. The Jeep then travels 1/3 of a unit
(expending 1/3 of a drum of fuel), refills the tank using the 1/3 of a
drum of fuel stored there, and continues an additional 1 unit of distance
on a full tank, giving a total distance of 4/3. The solutions for n
= 1, 2, ... drums are 1, 4/3, 23/15, 176/105, 563/315, ..., which can also
be written as 
,
 |
|
 |
|
 |
|
 |
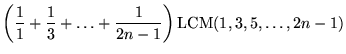(Sloane's A025550 and A025547).
Alway, G. C. "Crossing the Desert." Math. Gaz. 41, 209, 1957.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 32, 1987.
Bellman, R. Exercises 54-55 Dynamic Programming. Princeton, NJ: Princeton University Press, p. 103, 1955.
Fine, N. J. "The Jeep Problem." Amer. Math. Monthly 54, 24-31, 1947.
Gale, D. "The Jeep Once More or Jeeper by the Dozen." Amer. Math. Monthly 77, 493-501, 1970.
Gardner, M. The Second Scientific American Book of Mathematical Puzzles & Diversions: A New Selection. New York: Simon and Schuster, pp. 152 and 157-159, 1961.
Haurath, A.; Jackson, B.; Mitchem, J.; and Schmeichel, E. "Gale's Round-Trip Jeep Problem." Amer. Math. Monthly 102, 299-309, 1995.
Helmer, O. "A Problem in Logistics: The Jeep Problem." Project Rand Report No. Ra 15015, Dec. 1947.
Phipps, C. G. "The Jeep Problem, A More General Solution." Amer. Math. Monthly 54, 458-462, 1947.
Sloane, N. J. A. Sequences A025550 and A025547 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
 | |||
|
| ||